
【题目】如图,抛物线y=x2+bx+c与x轴交于A,B两点,且点A在点B的左侧,直线y=﹣x﹣1与抛物线交于A,C两点,其中点C的横坐标为2.
(1)求二次函数的解析式;
(2)P是线段AC上的一个动点,过点P作y轴的平行线交抛物线于点E,求线段PE长度的最大值.

【答案】(1)y=x2﹣2x﹣3.(2)当m=![]() 时,PE取最大值,最大值为
时,PE取最大值,最大值为![]() .
.
【解析】分析: (1)根据点C在x轴上求得点A的坐标,再根据点C的横坐标为2求出点C的纵坐标,把A(-1,0),B(3,0)代入二次函数的解析式,利用待定系数法即可求得函数的解析式;
(2)设点P的坐标为(m,-m-1)(-1≤m≤2),则点E的坐标为(m,m2-2m-3),进而可得出PE=-m2+m+2=-(m- ![]() )2+
)2+ ![]() ,再利用二次函数的性质即可解决最值问题.
,再利用二次函数的性质即可解决最值问题.
详解:
(1)当y=0时,有﹣x﹣1=0,
解得:x=﹣1,
∴点A的坐标为(﹣1,0);
当x=2时,y=﹣x﹣1=﹣3,
∴点C的坐标为(2,﹣3).
将A(﹣1,0)、C(2,﹣3)代入y=x2+bx+c,得:![]() ,
,
解得:![]() ,
,
∴二次函数的解析式为y=x2﹣2x﹣3.
(2)设点P的坐标为(m,﹣m﹣1)(﹣1≤m≤2),则点E的坐标为(m,m2﹣2m﹣3),
∴PE=﹣m﹣1﹣(m2﹣2m﹣3)=﹣m2+m+2=﹣(m﹣![]() )2+
)2+![]() .
.
∵﹣1<0,
∴当m=![]() 时,PE取最大值,最大值为
时,PE取最大值,最大值为![]() .
.
点睛: 本题考查了抛物线与x轴的交点、一次函数图象上点的坐标特征、二次函数的性质、二次函数图象上点的坐标特征、二次函数的最值以及待定系数法求二次函数解析式;解题的关键是:(1)利用一次函数图象上点的坐标特征求出点A、C的坐标;(2)用含m的代数式表示出PE的值.


 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
【题目】市政府要求武汉轻轨二七路段工程12个月完工。现由甲、乙两工程队参与施工,已知甲队单独完成需要16个月,每月需费用600万元;乙队单独完成需要24个月,每月需费用400万元。由于前期工程路面较宽,可由甲、乙两队共同施工。随着工程的进行,路面变窄,两队再同时施工,对交通影响较大,为了减小对解放大道的交通秩序的影响,后期只能由一个工程队施工.工程总指挥部结合实际情况现拟定两套工程方案:
①先由甲、乙两个工程队合做m个月后,再由甲队单独施工,保证恰好按时完成.
②先由甲、乙两个工程队合做n个月后,再由乙队单独施工,也保证恰好按时完成.
⑴求两套方案中m和n的值;
⑵通过计算,并结合施工费用及施工对交通的影响,你认为该工程总指挥部应该选择哪种方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:
①两个数互为倒数,则它们的乘积为![]() ;②若
;②若![]() ,
,![]() 互为相反数,则
互为相反数,则![]() ;
;
③![]() 个有理数相乘,如果负因数的个数为奇数个,则积为负;④若
个有理数相乘,如果负因数的个数为奇数个,则积为负;④若![]() ,则
,则![]() .其中正确的个数为( )
.其中正确的个数为( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个不同的数用大括号围起来,中间用逗号断开,如:{3,4},{-3,6,8,18},我们称之为集合,其中大括号内的数称其为集合的元素,如果一个集合满足:只要其中有一个元素a,使得-2a+4也是这个集合的元素,这样的集合我们称为条件集合,例如:集合{3,2},因为-2×3+4=-2,-2恰好是这个集合的元素,所以{3,-2}是条件集合:例如:集合{-2,9,8},因为-2×(-2)+4=8,8恰好是这个集合的元素,所以{-2,9,8}是条件集合.
(1)集合{-4,12}______条件集合;集合{![]() ,-
,-![]() ,
,![]() }______条件集合 (填“是”或“不是”)
}______条件集合 (填“是”或“不是”)
(2)若集合{8,10,n}是条件集合,求n的所有可能值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点M、N表示的数分别为a、b,我们把a、b之差的绝对值叫做点M、N之间的距离,即MN=│a-b│.已知数轴上三点A、O、B表示的数分别为-3,0,1,点P为数轴上任意一点,其表示的数为x.
![]()
(1)如果点P到点A、点B的距离相等,那么x=_______;
(2)当x是多少时,点P到点A、点B的距离之和是6;
(3)若点P以每秒3个单位长度的速度从点O沿着数轴的负方向运动时,点E以每秒1个单位长度的速度从点A沿着数轴的负方向运动,点F以每秒4个单位长度的速度从点B沿着数轴的负方向运动,且三个点同时出发,那么运动几秒时,点P到点E、点F的距离相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
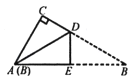
【题目】如图,有一直角三角形纸片ABC,∠C=90°,∠B=30°,将该直角三角形纸片沿DE折叠,使点B与点A重合,DE=1,则BC的长度为( )
A. 2 B. ![]() +2 C. 3 D. 2
+2 C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
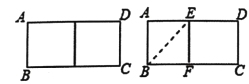
【题目】邻边不相等的矩形纸片,剪去一个正方形,余下一个四边形,称为第一次操作;在余下的四边形中减去一个正方形,又余下一个四边形,称为第二次操作;…,以此类推,若第n次操作后余下的四边形是正方形,则称原矩形是n阶矩形.如图,矩形ABCD中,若AB=1,AD=2,则矩形ABCD是1阶矩形.已知一个矩形是2阶矩形,较短边长为2,则较长边的长度为( )
A. 6 B. 8 C. 5或8 D. 3或6
查看答案和解析>>
科目:初中数学 来源: 题型:
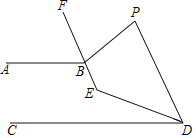
【题目】如图已知AB∥CD,P为直线AB,CD外一点,BF平分∠ABP,DE平分∠CDP,BF的反向延长线交DE于点E.
(1)∠ABP,∠P和∠PDC的数量关系为 ;
(2)若∠BPD=80°,求∠BED的度数;
(3)∠P与∠E的数量关系为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com