
【题目】如图直角坐标系中,矩形ABCD的边BC在x轴上,点B、D的坐标分别为B(1,0),D(3,3).
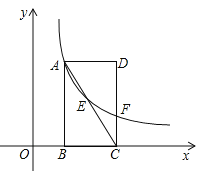
(1)点C的坐标 ;
(2)若反比例函数![]() 的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
的图象经过直线AC上的点E,且点E的坐标为(2,m),求m的值及反比例函数的解析式;
(3)若(2)中的反比例函数的图象与CD相交于点F,连接EF,在直线AB上找一点P,使得![]() ,求点P的坐标.
,求点P的坐标.
【答案】(1)C(3,0);(2)![]() ,
, ![]() ;(3)(1,0.5)或(1,3.5)
;(3)(1,0.5)或(1,3.5)
【解析】(1)由D点坐标得;(2)求出直线AC的解析式,把E的坐标代入求出m的值,从而求得反比例函数的解析式;(3)延长FC至M,使CM=![]() CF,连接EM,过点M作直线MP∥EF交直线AB于P,求出直线EF的解析式,得出直线PM的解析式,从而求出点P的坐标.
CF,连接EM,过点M作直线MP∥EF交直线AB于P,求出直线EF的解析式,得出直线PM的解析式,从而求出点P的坐标.
解:(1)C(3,0)
(2)设直线AC的解析式为![]() ,则
,则
![]() ,解得:
,解得: 
∴直线AC的解析式为![]()
∵点E(2, ![]() )在直线AC上, ∴
)在直线AC上, ∴![]() ,
,
∴点E(2, ![]() )
)
∵反比例函数![]() 的图象经过点E,∴
的图象经过点E,∴![]() ,
,
∴反比例函数的解析式为 ![]()
(3)延长FC至M,使CM=![]() CF,连接EM,则S△EFM =
CF,连接EM,则S△EFM =![]() S△EFC,M(3,-0.5)
S△EFC,M(3,-0.5)
在![]() 中,当
中,当![]() 时,
时, ![]() ,∴F(3,1)
,∴F(3,1)
过点M作直线MP∥EF交直线AB于P,则S△PEF=S△MEF
设直线EF的解析式为![]() 解得
解得 ,∴
,∴![]()
设直线PM的解析式为![]() ,代入M(3,-0.5)得:
,代入M(3,-0.5)得: ![]()
∴![]()
当![]() 时
时![]() ,∴点P(1,0.5)
,∴点P(1,0.5)
同理可得点P(1,3.5)
∴点P坐标为(1,0.5)或(1,3.5)
点晴:本题主要考查一次函数与反比例函数的图象和性质并与几何图形结合在一起的综合应用题.其重点是让学生运用待定系数法求函数解析式,难点是第3个问题,通过动手操作让学生猜想并求出满足条件的P的坐标,体现出学生综合运用知识解决实际问题的能力,而突破难点的关键在于利用平行线间的距离处处相等,从而实现等面积的转换.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】七年级学生小聪和小明完成了数学实验《钟面上的数学》之后,自制了一个模拟钟面,如图所示,O为模拟钟面圆心,M、O、N在一条直线上,指针OA、OB分别从OM、ON出发绕点O转动,OA运动速度为每秒15°,OB运动速度为每秒5°,当一根指针与起始位置重合时,运动停止,设转动的时间为t秒,请你试着解决他们提出的下列问题: 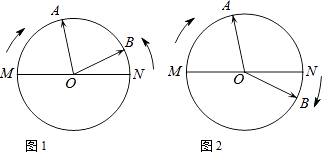
(1)若OA顺时针转动,OB逆时针转动,t=秒时,OA与OB第一次重合;
(2)若它们同时顺时针转动,
①当 t=2秒时,∠AOB=°;
②当t为何值时,OA与OB第一次重合?
③当t为何值时,∠AOB=30°?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB边的垂直平分线l交BC于点D,AC边的垂直平分线l2交BC于点E,l与 l2相交于点O,连接AD,AE,△ADE的为6cm.
(1)求BC的长;
(2)分别连接OA,OB,OC,若△OBC的周长为16cm,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1∥l2 , 点A是l1上的动点,点B在l1上,点C、D在l2上,∠ABC,∠ADC的平分线交于点E(不与点B,D重合).
(1)若点A在点B的左侧,∠ABC=80°,∠ADC=60°,过点E作EF∥l1 , 如图①所示,求∠BED的度数. 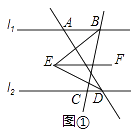
(2)若点A在点B的左侧,∠ABC=α°,∠ADC=60°,如图②所示,求∠BED的度数;(直接写出计算的结果) 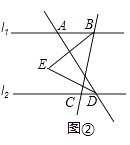
(3)若点A在点B的右侧,∠ABC=α°,∠ADC=60°,如图③所示,求∠BED的度数. 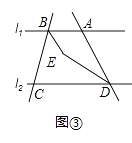
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
为了提高产品的附加值,某公司计划将研发生产的1200件新产品进行精加工后再投放市场.现有甲、乙两个工厂都具备加工能力,公司派出相关人员分别到这两个工厂了解情况,获得如下信息:
信息一:甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天;
信息二:乙工厂每天加工的数量是甲工厂每天加工数量的1.5倍.
根据以上信息,求甲、乙两个工厂每天分别能加工多少件新产品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江苏卫视《最强大脑》曾播出一期“辨脸识人”节目,参赛选手以家庭为单位,每组家庭由爸爸妈妈和宝宝3人组成,爸爸、妈妈和宝宝分散在三块区域,选手需在宝宝中选一个宝宝,然后分别在爸爸区域和妈妈区域中正确找出这个宝宝的父母,不考虑其他因素,仅从数学角度思考,已知在本期比赛中有A、B、C三组家庭进行比赛.
(1)若机器人智能小度选择A组家庭的宝宝,求小度在妈妈区域中正确找出其妈妈的概率;
(2)如果任选一个宝宝(假如选A组家庭),通过列表或树状图的方法,求机器人智能小度至少正确找对宝宝父母其中一人的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com