
【题目】已知:A(0,1),B(2,0),C(4,3) 
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
【答案】
(1)解:如图所示:

(2)解:过点C向x、y轴作垂线,垂足为D、E.
∴四边形DOEC的面积=3×4=12,△BCD的面积= ![]() =3,△ACE的面积=
=3,△ACE的面积= ![]() =4,△AOB的面积=
=4,△AOB的面积= ![]() =1.
=1.
∴△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积
=12﹣3﹣4﹣1=4.
(3)解:当点p在x轴上时,△ABP的面积= ![]() =4,即:
=4,即: ![]() ,解得:BP=8,
,解得:BP=8,
所点P的坐标为(10,0)或(﹣6,0);
当点P在y轴上时,△ABP的面积= ![]() =4,即
=4,即 ![]() ,解得:AP=4.
,解得:AP=4.
所以点P的坐标为(0,5)或(0,﹣3).
所以点P的坐标为(0,5)或(0,﹣3)或(10,0)或(﹣6,0).
【解析】(1)确定出点A、B、C的位置,连接AC、CB、AB即可;(2)过点C向x、y轴作垂线,垂足为D、E,△ABC的面积=四边形DOEC的面积﹣△ACE的面积﹣△BCD的面积﹣△AOB的面积;(3)当点p在x轴上时,由△ABP的面积=4,求得:BP=8,故此点P的坐标为(10,0)或(﹣6,0);当点P在y轴上时,△ABP的面积=4,解得:AP=4.所以点P的坐标为(0,5)或(0,﹣3).
【考点精析】本题主要考查了三角形的面积的相关知识点,需要掌握三角形的面积=1/2×底×高才能正确解答此题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别在边AC,AB上,BD与CE交于点O,给出下列三个条件:①∠EBO=∠DCO;②BE=CD;③OB=OC. 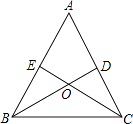
(1)上述三个条件中,由哪两个条件可以判定△ABC是等腰三角形?(用序号写出所有成立的情形)
(2)请选择(1)中的一种情形,写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
(1)求证:AE=AF;
(2)求∠EAF的度数.
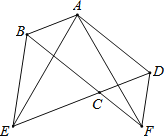
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中x和y的值如下表:( )
x | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
y | -5.6 | -3.1 | -1.5 | 0.9 | 1.8 |
则ax2+bx+c=0的一个根的范围是( )
A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC , D为边BC上一点,以AB、BD为邻边作平行四边形ABDE , 连接AD、EC . 若BD=CD , 求证:四边形ADCE是矩形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com