
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:![]() .
.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2,即2CD2=AD2+DB2.
试题解析:(1)∵△ABC和△ECD都是等腰直角三角形,∴AC=BC,CD=CE,∵∠ACB=∠DCE=90°,∴∠ACE+∠ACD=∠BCD+∠ACD,∴∠ACE=∠BCD,在△ACE和△BCD中,∵AC=BC,∠ACE=∠BCD ,CD=CE,∴△AEC≌△BDC(SAS);
(2)∵△ACB是等腰直角三角形,∴∠B=∠BAC=45度.∵△ACE≌△BCD,∴∠B=∠CAE=45°,∴∠DAE=∠CAE+∠BAC=45°+45°=90°,∴![]() .
.
由(1)知AE=DB,∴![]() ,即
,即![]() .
.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:初中数学 来源: 题型:
【题目】已知:A(0,1),B(2,0),C(4,3) 
(1)在坐标系中描出各点,画出△ABC.
(2)求△ABC的面积;
(3)设点P在坐标轴上,且△ABP与△ABC的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣![]() x2﹣
x2﹣![]() x+2与x轴交于A、B两点,与y轴交于点C
x+2与x轴交于A、B两点,与y轴交于点C
(1)求点A,B,C的坐标;
(2)点E是此抛物线上的点,点F是其对称轴上的点,求以A,B,E,F为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点M,使得△ACM是等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠DAB+∠D=180°,AC平分∠DAB,且∠CAD=25°,∠B=95°.求:∠DCE和∠DCA的度数. 
请将以下解答补充完整,
解:因为∠DAB+∠D=180°
所以DC∥AB()
所以∠DCE=∠B()
又因为∠B=95°,
所以∠DCE=°;
因为AC平分∠DAB,∠CAD=25°,根据角平分线定义,
所以∠CAB==°,
因为DC∥AB
所以∠DCA=∠CAB,()
所以∠DCA=°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( ) 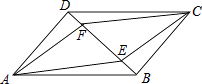
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=﹣x+3与直线l2:y=x+1相交于点A.并且l1交x轴于点B,l2交x轴于点C.若平面上有一点D,构成平行四边形ABDC,请写出D点坐标 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com