
【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( ) 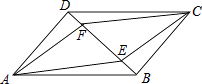
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
【答案】D
【解析】解:如图,连接AC与BD相交于O, 在ABCD中,OA=OC,OB=OD,
要使四边形AECF为平行四边形,只需证明得到OE=OF即可;
A、若BE=DF,则OB﹣BE=OD﹣DF,即OE=OF,故本选项错误;
B、若AF⊥BD,CE⊥BD,则可以利用“角角边”证明△ADF和△CBE全等,从而得到DF=BE,然后同A,故本选项错误;
C、∠BAE=∠DCF能够利用“角角边”证明△ABE和△CDF全等,从而得到DF=BE,然后同A,故本选项错误;
D、AF=CE无法证明得到OE=OF,故本选项正确.
故选D.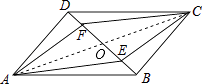
【考点精析】根据题目的已知条件,利用平行四边形的判定与性质的相关知识可以得到问题的答案,需要掌握若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.


科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c中x和y的值如下表:( )
x | 0.10 | 0.11 | 0.12 | 0.13 | 0.14 |
y | -5.6 | -3.1 | -1.5 | 0.9 | 1.8 |
则ax2+bx+c=0的一个根的范围是( )
A.0.10<x<0.11B.0.11<x<0.12C.0.12<x<0.13D.0.13<x<0.14
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,点D为斜边AB的中点,BC=6,CD=5,过点A作AE⊥AD且AE=AD,过点E作EF垂直于AC边所在的直线,垂足为点F,连接DF,请你画出图形,并直接写出线段DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
(1)求证:△ACE≌△BCD;
(2)求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
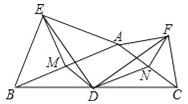
【题目】如图,在钝角△ABC中,点D是BC的中点,分别以AB和AC为斜边向△ABC的外侧作等腰直角三角形ABE和等腰直角三角形ACF,M、N分别为AB、AC的中点,连接DM、DN、DE、DF、EM、EF、FN.求证:
(1)△EMD≌△DNF;
(2)△EMD∽△EAF;
(3)DE⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O为直线AD上一点,射线OC,射线OB,∠AOC与∠AOB互补,OM,ON分别为∠AOC,∠AOB的平分线,若∠MON=40°.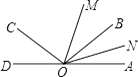
(1)∠COD与∠AOB相等吗?请说明理由;
(2)试求∠AOC与∠AOB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com