
【题目】如图,在ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC.求证:∠BAC=∠BFC. 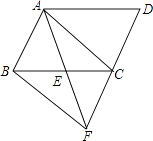
【答案】证明:∵四边形ABCD是平行四边形, ∴AB∥CD,
∵点F为DC的延长线上的一点,
∴AB∥DF,
∴∠BAE=∠CFE,∠ECF=∠EBA,
∵E为BC中点,
∴BE=CE,
在△BAE和△CFE中,  ,
,
∴△BAE≌△CFE,
∴AB=CF,
又∵AB∥CF,
∴四边形ABFC是平行四边形,
∴∠BAC=∠BFC.
【解析】根据平行四边形的性质可得到AB∥CD,从而可得到AB∥DF,得出∠BAE=∠CFE,∠ECF=∠EBA,由AAS证明△BAE≌△CFE,根据全等三角形的对应边相等可证得AB=CF,证出四边形ABFC是平行四边形,即可得出结论.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( ) 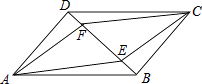
A.BE=DF
B.AF⊥BD,CE⊥BD
C.∠BAE=∠DCF
D.AF=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E(与点B、C不重合)是BC边上一点,将线段EA绕点E顺时针旋转90°到EF,过点F作BC的垂线交BC的延长线于点G,连接CF.
(1)求证:△ABE≌△EGF;
(2)若AB=2,S△ABE=2S△ECF,求BE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同庆中学为丰富学生的校园生活,准备从军跃体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球、一个篮球各需多少元?
(2)根据同庆中学的实际情况,需从军跃体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com