
如图,在正方形ABCD中,E、F分别为BC、AB上两点,且BE=BF,过点B作AE的垂线交AC于点G,过点G作CF的垂线交BC于点H延长线段AE、GH交于点M.
(1)求证:∠BFC=∠BEA;
(2)求证:AM=BG+GM。
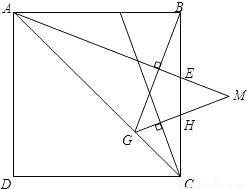
(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)根据正方形的四条边都相等,AB=BC,又BE=BF,所以△ABE和△CBF全等,再根据全等三角形对应角相等即可证出;
(2)连接DG,根据正方形的性质,AB=AD,∠DAC=∠BAC=45°,AG是公共边,所以△ABG和△ADG全等,根据全等三角形对应边相等,BG=DG,对应角相等∠2=∠3,因为BG⊥AE,所以∠BAE+∠2=90°,而∠BAE+∠4=90°,所以∠2=∠4,因此∠3=∠4,根据GM⊥CF和(1)中全等三角形的对应角相等可以得到∠1=∠BFC=∠2,在△ADG中,∠DGC=∠3+45°,所以DGM三点共线,因此△ADM是等腰三角形,AM=DM=DG+GM,所以AM=BG+GM.
(1)在正方形ABCD中,AB=BC,∠ABC=90°,
在△ABE和△CBF中,
 ,
,
∴△ABE≌△CBF(SAS),
∴∠BFC=∠BEA;
(2)连接DG,
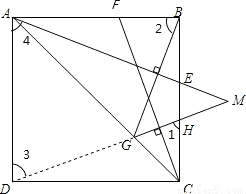
在△ABG和△ADG中,
 ,
,
∴△ABG≌△ADG(SAS),
∴BG=DG,∠2=∠3,
∵BG⊥AE,
∴∠BAE+∠2=90°,
∵∠BAD=∠BAE+∠4=90°,
∴∠2=∠3=∠4,
∵GM⊥CF,
∴∠BCF+∠1=90°,
又∠BCF+∠BFC=90°,
∴∠1=∠BFC=∠2,
∴∠1=∠3,
在△ADG中,∠DGC=∠3+45°,
∴∠DGC也是△CGH的外角,
∴D、G、M三点共线,
∵∠3=∠4(已证),
∴AM=DM,
∵DM=DG+GM=BG+GM,
∴AM=BG+GM.
考点:1.正方形的性质;2.全等三角形的判定与性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题(一)数学试卷(解析版) 题型:填空题
如图,⊙O的直径AB与弦AC的夹角∠A=30°,过点C作⊙O的切线交AB的延长线于点P,PC=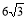 ,则图中阴影部分的面积为 (结果保留π).
,则图中阴影部分的面积为 (结果保留π).

查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题二数学试卷(解析版) 题型:选择题
如图,在平面直角坐标系中,直线y=2x+4与 轴、
轴、 轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线
轴分别交于A、B两点,以AB为边在第二象限作正方形ABCD,点D在双曲线 上,将正方形ABCD沿
上,将正方形ABCD沿 轴正方向平移
轴正方向平移 个单位长度后,点C恰好落在此双曲线上,则
个单位长度后,点C恰好落在此双曲线上,则 的值是( ).
的值是( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市万州区岩口复兴学校九年级下学期期中命题三数学试卷(解析版) 题型:选择题
如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣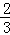 ;④3≤n≤4中,正确的是( )。
;④3≤n≤4中,正确的是( )。
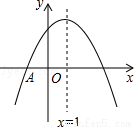
A.①② B.③④ C.①④ D.①③
查看答案和解析>>
科目:初中数学 来源:2013-2014学年重庆市九年级下学期期中考试数学试卷(解析版) 题型:选择题
如图,⊙O是△ABC的外接圆,∠OCB=50°,则∠A的度数等于( )

A.40° B.50° C.60° D.70°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com