解:(1)由已知点M(

,0),N(0,6),经过M、N两点的直线可得:
∠OMN=30°,
故答案为:30°.
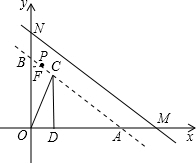
(2)作PF⊥y轴于F.
∵M(

,0),N(0,6),
∴∠NMO=30°,
∴∠BAO=30°.
在直角三角形PFB中,PB=t,∠BPF=30°,
则BF=

,PF=

t.
又∵NB=t,
∴OF=ON-NB-BF=6-t-

=6-

t,
则P点的坐标为(

t,6-

t).
(3)此题应分为两种情况:
①当⊙P和OC第一次相切时,
设直线BP与OC的交点是G.
根据题意,知∠BOC=∠BAO=30°.
则BC=

OB=3-

,
则PG=3-

t.
根据直线和圆相切,则圆心到直线的距离等于圆的半径,得
3-

t=1,t=

.
此时⊙P与直线CD显然相离;
②当⊙P和OC第二次相切时,
则有

t-3=1,t=

.
此时⊙P与直线CD显然相交.
答:当t=

或

时⊙P和OC相切,t=

时⊙P和直线CD相离,当t=

时⊙P和直线CD相交.
分析:(1)由已知点M(

,0),N(0,6),经过M、N两点的直线,利用直角三角形可求出∠OMN;
(2)过点P向y轴引垂线.根据已知点A、B的坐标可以求得∠BAO=30°,从而可以结合题意,利用解直角三角形的知识进行求解;
(3)此题应分作两种情况考虑:
①当P位于OC左侧,⊙P与OC第一次相切时,易证得∠COB=∠BAO=30°,设直线l与OC的交点为G,根据∠BOC的度数,即可求得BG、PG的表达式,而此时⊙P与OC相切,可得PM=1,由此可列出关于t的方程,求得t的值,进而可判断出⊙P与CD的位置关系;
点评:此题考查的知识点是一次函数综合题,综合考查了解直角三角形、直线和圆的位置关系等知识的综合应用能力,难度较大.

 ,0),N(0,6),经过M、N两点的直线 l以每秒1个单位的速度向下作匀速平移运动,分别交x轴、y轴于A、B两点,与此同时,点P从点N出发,在直
,0),N(0,6),经过M、N两点的直线 l以每秒1个单位的速度向下作匀速平移运动,分别交x轴、y轴于A、B两点,与此同时,点P从点N出发,在直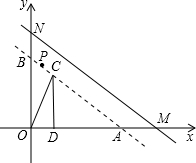 线l上以每秒1个单位的速度沿直线l向右下方作匀速运动,设它们运动的时间为t秒.
线l上以每秒1个单位的速度沿直线l向右下方作匀速运动,设它们运动的时间为t秒. 解:(1)由已知点M(
解:(1)由已知点M( ,0),N(0,6),经过M、N两点的直线可得:
,0),N(0,6),经过M、N两点的直线可得: ,0),N(0,6),
,0),N(0,6), ,PF=
,PF= t.
t. =6-
=6- t,
t, t,6-
t,6- t).
t). OB=3-
OB=3- ,
, t.
t. t=1,t=
t=1,t= .
. t-3=1,t=
t-3=1,t= .
. 或
或  时⊙P和OC相切,t=
时⊙P和OC相切,t= 时⊙P和直线CD相离,当t=
时⊙P和直线CD相离,当t= 时⊙P和直线CD相交.
时⊙P和直线CD相交. ,0),N(0,6),经过M、N两点的直线,利用直角三角形可求出∠OMN;
,0),N(0,6),经过M、N两点的直线,利用直角三角形可求出∠OMN;

 阅读快车系列答案
阅读快车系列答案 如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( )
如图,已知点A、B、C、D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为( ) 如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设
如图,已知点D为△ABC中AC边上一点,且AD:DC=3;4,设