

分析 (1)由菱形的性质得出BA=BC,∠ABD=∠CBD.由SAS证明△ABE≌△CBE,即可得出结论.
(2)联结AC,交BD于点O,过点A作AH⊥BC于H,过点E作EF⊥BC于F,由菱形的性质得出AC⊥BD.由三角函数求出AO=OC=2$\sqrt{5}$,BO=OD=4$\sqrt{5}$.由菱形面积得出AH=8,BH=6.由相似三角形的性质得出比例式,求出EF的长,即可得出答案;
(3)因为点P在线段BC的延长线上,所以∠EPC不可能为直角.分情况讨论:
①当∠ECP=90°时,②当∠CEP=90°时,由全等三角形的性质和相似三角形的性质即可得出答案.
解答 (1)证明:∵四边形ABCD是菱形,
∴BA=BC,∠ABE=∠CBE.
在△ABE和△CBE中,$\left\{\begin{array}{l}{BA=BC}&{\;}\\{∠ABE=∠CBE}&{\;}\\{BE=BE}&{\;}\end{array}\right.$,
又∵BE=BE,
∴△ABE≌△CBE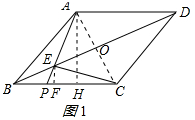
∴AE=CE.
(2)解:连接AC,交BD于点O,过点A作AH⊥BC,过点E作EF⊥BC,如图1所示:
垂足分别为点H、F.
∵四边形ABCD是菱形,
∴AC⊥BD.
∵AB=10,tan∠ABD=$\frac{AO}{BO}$=$\frac{1}{2}$,
∴AO=OC=2$\sqrt{5}$,BO=OD=4$\sqrt{5}$,AC=4$\sqrt{5}$,BD=8$\sqrt{5}$,
∵$\frac{1}{2}$AC•BD=BC•AH,
∴AH=8,∴BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=6.
∵AD∥BC,∵AD∥BC,
∴$\frac{AE}{EP}=\frac{AD}{BP}$,
∴$\frac{AE+EP}{EP}=\frac{AD+BP}{BP}$,
∴$\frac{AP}{EP}$=$\frac{10+x}{x}$,
∴$\frac{EP}{AP}$=$\frac{10+x}{x}$.
∵EF∥AH,
∴$\frac{EF}{AH}=\frac{EP}{AP}$,
∴EF=$\frac{8x}{10+x}$.
∴y=$\frac{1}{2}$PC′EF=$\frac{1}{2}$(10-x)•$\frac{8x}{10+x}$=$\frac{20x-4{x}^{2}}{10+x}$,
即y═$\frac{20x-4{x}^{2}}{10+x}$,(0<x<10).
(3)解:因为点P在线段BC的延长线上,所以∠EPC不可能为直角.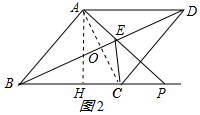 如图2所示:
如图2所示:
①当∠ECP=90°时
∵△ABE≌△CBE,
∴∠BAE=∠BCE=90°,
∵cos∠ABP=$\frac{AB}{BP}$=$\frac{BH}{AB}$,即$\frac{10}{BP}=\frac{3}{5}$
∴BP=$\frac{50}{3}$.
②当∠CEP=90°时,
∵△ABE≌△CBE,
∴∠AEB=∠CEB=45°,
∴AO=OE=2$\sqrt{5}$,
∴ED=2$\sqrt{5}$,BE=6$\sqrt{5}$.
∵AD∥BP,
∴$\frac{AD}{BP}=\frac{DE}{BE}$,
∴$\frac{10}{BP}=\frac{2\sqrt{5}}{6\sqrt{5}}$,
∴BP=30.
综上所述,当△EPC是直角三角形时,线段BP的长为$\frac{50}{3}$或30.
点评 本题是四边形综合题目,考查了菱形的性质、勾股定理、三角函数、全等三角形的判定与性质、相似三角形的判定与性质等知识;本题综合性强,有一定难度,证明三角形全等和三角形相似是解决问题的关键.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )
如图,已知点A(0,1),B(0,-1),以点A为圆心,AB为半径作圆,交x轴的正半轴于点C,则∠BAC等于( )| A. | 90° | B. | 120° | C. | 60° | D. | 30° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
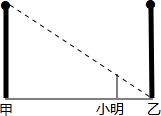 如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )
如图,甲、乙两盏路灯杆相距20米,一天晚上,当小明从灯甲底部向灯乙底部直行16米时,发现自己的身影顶部正好接触到路灯乙的底部.已知小明的身高为1.6米,那么路灯甲的高为( )| A. | 7米 | B. | 8米 | C. | 9米 | D. | 10米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
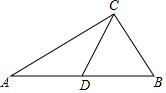 如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )
如图,在△ABC中,AC=4,BC=2,点D是边AB上一点,CD将△ABC分成△ACD和△BCD,若△ACD是以AC为底的等腰三角形,且△BCD与△BAC相似,则CD的长为( )| A. | $\frac{\sqrt{17}-1}{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | $\frac{4}{3}$$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com