
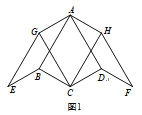
°æƒø°ø‘⁄Àƒ±þ–Œ ABCD÷–£¨AB£ΩAD£¨°œBAD£Ω60°„£¨±þBC»∆µ„BÀ≥ ±’Ζ˝◊™120°„µ√µΩBE£¨±þDC»∆µ„DƒÊ ±’Ζ˝◊™120°„µ√µΩDF£¨Àƒ±þ–ŒABEG∫ÕÀƒ±þ–ŒADFHŒ™∆Ω––Àƒ±þ–Œ£Æ
£®1£©»ÁÕº1£¨»ÙBC£ΩCD£¨°œBCD£Ω120°„£¨‘Ú°œGCH£Ω_______°„£ª
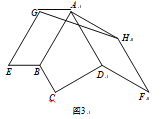
£®2£©»ÁÕº2£¨»ÙBC°ŸCD£¨ÃΩæø°œGCHµƒ¥Û–° «∑Ò∑¢…˙±‰ªØ£¨≤¢÷§√˜ƒ„µƒΩ·¬€£ª
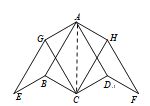
£®3£©»ÁÕº3£¨»Ù°œBCD£Ω°œADC£Ω90°„£¨AB£Ω![]() «Î÷±Ω”–¥≥ˆ°˜AGHµƒ÷Ð≥§£Æ
«Î÷±Ω”–¥≥ˆ°˜AGHµƒ÷Ð≥§£Æ

°æ¥∞∏°ø£®1£©60£ª£®2£©≤ª±‰£¨¿Ì”…º˚Ω‚Œˆ£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
£®1£©¡¨Ω”AC£¨÷§√˜![]()
![]() £¨º¥ø…µ√
£¨º¥ø…µ√![]() £ª
£ª
£®2£©≤ª±‰£¨![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨
£¨![]() £¨µ√µΩ
£¨µ√µΩ![]() Œ™µ»±þ»˝Ω«–Œ£¨”÷“ÚŒ™Àƒ±þ–Œ
Œ™µ»±þ»˝Ω«–Œ£¨”÷“ÚŒ™Àƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£¨ø…µ√
«∆Ω––Àƒ±þ–Œ£¨ø…µ√![]() £¨
£¨![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨À˘“‘
£¨À˘“‘![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨
£¨![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨º¥
£¨º¥![]() £¨
£¨
ø…÷§![]() £¨µ√µΩ
£¨µ√µΩ![]() £¨
£¨![]() £¨Õ¨¿Ìø…µ√£¨
£¨Õ¨¿Ìø…µ√£¨![]() £¨ µ√
£¨ µ√![]() £¨
£¨![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨
£¨![]() £¨
£¨![]() £¨À˘“‘
£¨À˘“‘![]() £¨“ÚŒ™
£¨“ÚŒ™![]() £¨
£¨![]() £¨
£¨![]() £¨ø…÷§
£¨ø…÷§![]() £¨ø…µ√
£¨ø…µ√![]() £¨
£¨![]() £¨”…µ»¡øπÿœµø…µ√
£¨”…µ»¡øπÿœµø…µ√![]() £ª
£ª
£®3£©∑÷±«Û≥ˆAG°¢AH°¢GHµƒ≥§£¨÷±Ω”œýº”º¥ø…£ª
Ω‚£∫£®1£©»ÁÕº£¨¡¨Ω”AC£¨
‘⁄![]() ∫Õ
∫Õ![]() ÷–£¨
÷–£¨
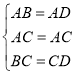 £¨
£¨
°ý![]()
![]() £¨
£¨
°ý![]() £ª
£ª
£®2£©≤ª±‰£¨![]() £¨¿Ì”…»Áœ¬£∫
£¨¿Ì”…»Áœ¬£∫
¡¨Ω”![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨
°ý![]() Œ™µ»±þ»˝Ω«–Œ£¨
Œ™µ»±þ»˝Ω«–Œ£¨
°þÀƒ±þ–Œ![]() «∆Ω––Àƒ±þ–Œ£¨
«∆Ω––Àƒ±þ–Œ£¨
![]() £¨
£¨![]() £¨
£¨
°þ![]() £¨
£¨
![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨
Õ¨¿Ìø…µ√£¨![]() £¨
£¨
![]() £¨
£¨![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨![]() £¨
£¨
![]() £¨
£¨
![]() £¨
£¨
°þ![]() £¨
£¨![]() £¨
£¨
£®3£©![]() £Æ
£Æ


 ”¿«¨ΩÔ˝∫ƺŸ◊˜“µøÏ¿÷ºŸ∆⁄—”±þ»À√Ò≥ˆ∞Ê…Áœµ¡–¥∞∏
”¿«¨ΩÔ˝∫ƺŸ◊˜“µøÏ¿÷ºŸ∆⁄—”±þ»À√Ò≥ˆ∞Ê…Áœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ![]() ÷–£¨“—÷™µ„
÷–£¨“—÷™µ„![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨“‘
÷·…œ£¨“‘![]() Œ™÷±æ∂◊˜
Œ™÷±æ∂◊˜![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨«“‘⁄µ„
÷·…œ£¨«“‘⁄µ„![]() …œ∑Ω£¨π˝µ„
…œ∑Ω£¨π˝µ„![]() ◊˜
◊˜![]() µƒ«–œþ
µƒ«–œþ![]() £¨
£¨![]() Œ™«–µ„£¨»Áπ˚µ„
Œ™«–µ„£¨»Áπ˚µ„![]() ‘⁄µ⁄“ªœÛœÞ£¨‘Ú≥∆
‘⁄µ⁄“ªœÛœÞ£¨‘Ú≥∆![]() Œ™µ„
Œ™µ„![]() µƒ¿Îµ„£Æ¿˝»Á£¨Õº1÷–µƒ
µƒ¿Îµ„£Æ¿˝»Á£¨Õº1÷–µƒ![]() Œ™µ„
Œ™µ„![]() µƒ“ª∏ˆ¿Îµ„£Æ
µƒ“ª∏ˆ¿Îµ„£Æ
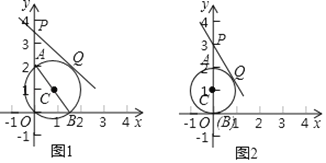
£®1£©“—÷™µ„![]() £¨
£¨![]() Œ™
Œ™![]() µƒ¿Îµ„£Æ
µƒ¿Îµ„£Æ
¢Ÿ»ÁÕº2£¨»Ù![]() £¨‘Ú‘≤–ƒ
£¨‘Ú‘≤–ƒ![]() µƒ◊¯±ÍŒ™__________£¨œþ∂Œ
µƒ◊¯±ÍŒ™__________£¨œþ∂Œ![]() µƒ≥§Œ™__________£ª
µƒ≥§Œ™__________£ª
¢⁄»Ù![]() £¨«Ûœþ∂Œ
£¨«Ûœþ∂Œ![]() µƒ≥§£ª
µƒ≥§£ª
£®2£©“—÷™![]() £¨÷±œþ
£¨÷±œþ![]() £Æ
£Æ
¢Ÿµ±![]() ±£¨»Ù÷±œþ
±£¨»Ù÷±œþ![]() …œ¥Ê‘⁄
…œ¥Ê‘⁄![]() µƒ¿Îµ„
µƒ¿Îµ„![]() £¨‘Úµ„
£¨‘Úµ„![]() ◊ð◊¯±Í
◊ð◊¯±Í![]() µƒ◊Ó¥Û÷µŒ™__________£ª
µƒ◊Ó¥Û÷µŒ™__________£ª
¢⁄º«÷±œþ![]() ‘⁄
‘⁄![]() µƒ≤ø∑÷Œ™Õº–Œ
µƒ≤ø∑÷Œ™Õº–Œ![]() £¨»Áπ˚Õº–Œ
£¨»Áπ˚Õº–Œ![]() …œ¥Ê‘⁄
…œ¥Ê‘⁄![]() µƒ¿Îµ„£¨÷±Ω”–¥≥ˆ
µƒ¿Îµ„£¨÷±Ω”–¥≥ˆ![]() µƒ»°÷µ∑∂Œß£Æ
µƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø£®∏–÷™£©»ÁÕº1£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨Ω´œþ∂Œ
£¨Ω´œþ∂Œ![]() »∆◊≈µ„
»∆◊≈µ„![]() ∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™
∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™![]() ÷¡œþ∂Œ
÷¡œþ∂Œ![]() £¨π˝µ„
£¨π˝µ„![]() ◊˜
◊˜![]() ÷·£¨¥π◊„Œ™µ„
÷·£¨¥π◊„Œ™µ„![]() £¨“◊÷™
£¨“◊÷™![]() £¨µ√µΩµ„
£¨µ√µΩµ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £Æ
£Æ
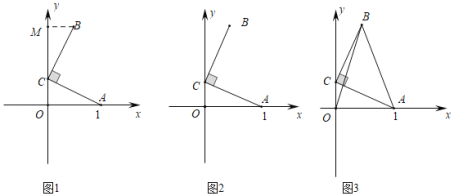
£®ÃΩæø£©»ÁÕº2£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨Ω´œþ∂Œ
£¨Ω´œþ∂Œ![]() »∆◊≈µ„
»∆◊≈µ„![]() ∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™
∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™![]() ÷¡œþ∂Œ
÷¡œþ∂Œ![]() £Æ
£Æ
£®1£©«Ûµ„![]() µƒ◊¯±Í£Æ£®”√∫¨
µƒ◊¯±Í£Æ£®”√∫¨![]() µƒ¥˙ ˝ Ω±Ì æ£©
µƒ¥˙ ˝ Ω±Ì æ£©
£®2£©«Û≥ˆBCÀ˘‘⁄÷±œþµƒ∫Ø ˝±Ì¥Ô Ω£Æ
£®Õÿ’𣩻ÁÕº3£¨‘⁄∆Ω√Ê÷±Ω«◊¯±Íœµ÷–£¨µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £¨µ„
£¨µ„![]() ‘⁄
‘⁄![]() ÷·…œ£¨Ω´œþ∂Œ
÷·…œ£¨Ω´œþ∂Œ![]() »∆◊≈µ„
»∆◊≈µ„![]() ∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™
∞¥ƒÊ ±’Î∑ΩœÚ–˝◊™![]() ÷¡œþ∂Œ
÷¡œþ∂Œ![]() £¨¡¨Ω·
£¨¡¨Ω·![]() °¢
°¢![]() £¨‘Ú
£¨‘Ú![]() µƒ◊Ó–°÷µŒ™_______£Æ
µƒ◊Ó–°÷µŒ™_______£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
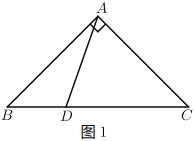
°æƒø°ø‘⁄![]() ÷–£¨
÷–£¨![]() £¨
£¨![]() £Æ
£Æ
£®1£©»ÁÕº1£¨»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ√ʪ˝£Æ
µƒ√ʪ˝£Æ
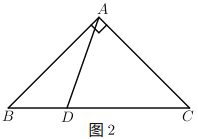
£®2£©»ÁÕº2£¨»Ù![]() Œ™œþ∂Œ
Œ™œþ∂Œ![]() …œ»Œ“‚“ªµ„£¨ÃΩæø
…œ»Œ“‚“ªµ„£¨ÃΩæø![]() £¨
£¨![]() £¨
£¨![]() »˝’þ÷ƺ‰µƒπÿœµ£¨≤¢÷§√˜£Æ
»˝’þ÷ƺ‰µƒπÿœµ£¨≤¢÷§√˜£Æ
£®3£©»ÁÕº3£¨»Ù![]() £¨
£¨![]() Œ™
Œ™![]() ƒ⁄“ªµ„£¨«Û
ƒ⁄“ªµ„£¨«Û![]() µƒ◊Ó–°÷µ£Æ
µƒ◊Ó–°÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
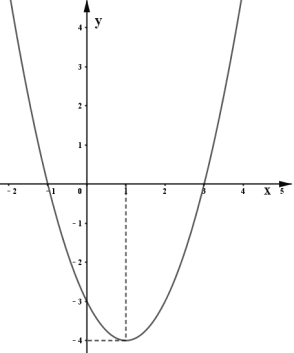
°æƒø°ø≈◊ŒÔœþy£Ωax2£´bx£´cµƒÕºœÛ»ÁÕºÀ˘ 棨∏˘æðÕºœÛªÿ¥Œ £Æ
£®1£©÷±Ω”–¥≥ˆx¬˙◊„ ≤√¥Ãıº˛ ±£¨yÀÊxµƒ‘ˆ¥Û∂¯‘ˆ¥Û£ª
£®2£©÷±Ω”–¥≥ˆ∑Ω≥Ãax2£´bx£´c£Ω0µƒ∏˘£ª
£®3£©÷±Ω”–¥≥ˆ≤ªµ» Ωax2£´bx£´c£º0 µƒΩ‚ºØ£ª
£®4£©»Ù∑Ω≥Ãax2£´bx£´c£´k£Ω1√ª”– µ ˝∏˘£¨÷±Ω”–¥≥ˆkµƒ»°÷µ∑∂Œß£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
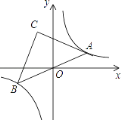
°æƒø°ø»ÁÕº£¨‘⁄∑¥±»¿˝∫Ø ˝y= ![]() µƒÕºœÛ…œ”–“ª∂ص„A£¨¡¨Ω”AO≤¢—”≥§ΩªÕºœÛµƒ¡Ì“ª÷ß”⁄µ„B£¨‘⁄µ⁄∂˛œÛœÞƒ⁄”–“ªµ„C£¨¬˙◊„AC=BC£¨µ±µ„A‘À∂Ø ±£¨µ„C º÷’‘⁄∫Ø ˝y=
µƒÕºœÛ…œ”–“ª∂ص„A£¨¡¨Ω”AO≤¢—”≥§ΩªÕºœÛµƒ¡Ì“ª÷ß”⁄µ„B£¨‘⁄µ⁄∂˛œÛœÞƒ⁄”–“ªµ„C£¨¬˙◊„AC=BC£¨µ±µ„A‘À∂Ø ±£¨µ„C º÷’‘⁄∫Ø ˝y= ![]() µƒÕºœÛ…œ‘À∂Ø£¨»Ùtan°œCAB=2£¨‘Úkµƒ÷µŒ™£® £©
µƒÕºœÛ…œ‘À∂Ø£¨»Ùtan°œCAB=2£¨‘Úkµƒ÷µŒ™£® £©
A. ©Å3 B. ©Å6 C. ©Å9 D. ©Å12
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝y=x2+bx+cµƒÕºœÒ”Îx÷·Ωª”⁄A£¨B¡Ωµ„£¨Bµ„◊¯±ÍŒ™(4,0)£¨”Îy÷·Ωª”⁄µ„C(0,4).µ„DŒ™≈◊ŒÔœþ…œ“ªµ„
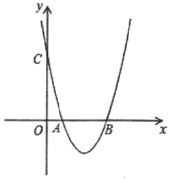
(1)«Û≈◊ŒÔœþµƒΩ‚Œˆ Ωº∞Aµ„◊¯±Í£ª
(2)»Ù°˜BCD «“‘BCŒ™÷±Ω«±þµƒ÷±Ω«»˝Ω«–Œ ±£¨«Ûµ„Dµƒ◊¯±Í£ª
(3)»Ù°˜BCD «»ÒΩ«»˝Ω«–Œ,«Î÷±Ω”–¥≥ˆµ„Dµƒ∫·◊¯±Ímµƒ»°÷µ∑∂Œß .
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∂‘”⁄ƒø°∞∂˛¥Œ∫Ø ˝y£Ω![]() £®x©Åm£©2+m£¨µ±2m©Å3°Ðx°Ð2m ±£¨yµƒ◊Ó–°÷µ «1£¨«Ûmµƒ÷µ£Æ°±º◊µƒΩ·π˚ «m£Ω1£¨““µƒΩ·π˚ «m£Ω©Å2£¨‘Ú£®°°°°£©
£®x©Åm£©2+m£¨µ±2m©Å3°Ðx°Ð2m ±£¨yµƒ◊Ó–°÷µ «1£¨«Ûmµƒ÷µ£Æ°±º◊µƒΩ·π˚ «m£Ω1£¨““µƒΩ·π˚ «m£Ω©Å2£¨‘Ú£®°°°°£©
A.º◊µƒΩ·π˚’˝»∑B.““µƒΩ·π˚’˝»∑
C.º◊°¢““µƒΩ·π˚∫œ‘⁄“ª∆≤≈’˝»∑D.º◊°¢““µƒΩ·π˚∫œ‘⁄“ª∆“≤≤ª’˝»∑
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
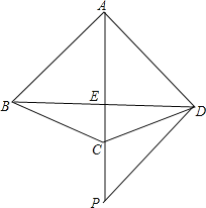
°æƒø°ø»ÁÕº£¨Àƒ±þ–ŒABCD÷–£¨AB=AC=AD£¨AC∆Ω∑÷°œBAD£¨µ„P «AC—”≥§œþ…œ“ªµ„£¨«“PD°ÕAD£Æ
£®1£©÷§√˜£∫°œBDC=°œPDC£ª
£®2£©»ÙAC”ÎBDœýΩª”⁄µ„E£¨AB=1£¨CE£∫CP=2£∫3£¨«ÛAEµƒ≥§£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com