
【题目】如图,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(4,0),与y轴交于点C(0,4).点D为抛物线上一点
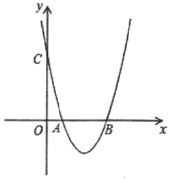
(1)求抛物线的解析式及A点坐标;
(2)若△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围 .
【答案】(1)y=x2-5x+4, A(1,0);(2)(6,10)或(2,-2);(3)3+![]() <m <6或 3-
<m <6或 3-![]() <m <2
<m <2
【解析】
(1)利用待定系数法求抛物线的解析式,再令y=0,求A的坐标;
(2)设D点横坐标为a,代入函数解析式可得纵坐标,分别讨论∠BCD=90°和∠CBD=90°的情况,作出图形进行求解;
(3)当BC为斜边构成Rt△BCD时,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',此时△BCD和△BCD'就是以BC为斜边的直角三角形,利用两点间距离公式列出方程求解,然后结合(2)找到m的取值范围.
(1)将B(4,0),C(0,4)代入y=x2+bx+c得,
![]() ,解得
,解得![]() ,
,
所以抛物线的解析式为![]() ,
,
令y=0,得![]() ,解得
,解得![]() ,
,![]() ,
,
∴A点的坐标为(1,0)
(2)设D点横坐标为![]() ,则纵坐标为
,则纵坐标为![]() ,
,
①当∠BCD=90°时,如下图所示,连接BC,过C点作CD⊥BC与抛物线交于点D,过D作DE⊥y轴与点E,
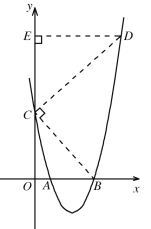
由B、C坐标可知,OB=OC=4,
∴△OBC为等腰直角三角形,
∴∠OCB=∠OBC=45°,
又∵∠BCD=90°,
∴∠ECD+∠OCB=90°
∴∠ECD=45°,
∴△CDE为等腰直角三角形,
∴DE=CE=a
∴OE=OC+CE=a+4
由D、E纵坐标相等,可得![]() ,
,
解得![]() ,
,![]() ,
,
当![]() 时,D点坐标为(0,4),与C重合,不符合题意,舍去.
时,D点坐标为(0,4),与C重合,不符合题意,舍去.
当![]() 时,D点坐标为(6,10);
时,D点坐标为(6,10);
②当∠CBD=90°时,如下图所示,连接BC,过B点作BD⊥BC与抛物线交于点D,过B作FG⊥x轴,再过C作CF⊥FG于F,过D作DG⊥FG于G,
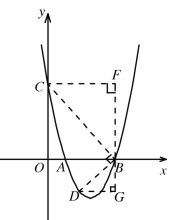
∵∠COB=∠OBF=∠BFC=90°,
∴四边形OBFC为矩形,
又∵OC=OB,
∴四边形OBFC为正方形,
∴∠CBF=45°
∵∠CBD=90°,
∴∠CBF+∠DBG=90°,
∴∠DBG=45°,
∴△DBG为等腰直角三角形,
∴DG=BG
∵D点横坐标为a,
∴DG=4-a,
而BG=![]()
∴![]()
解得![]() ,
,![]() ,
,
当![]() 时,D点坐标为(4,0),与B重合,不符合题意,舍去.
时,D点坐标为(4,0),与B重合,不符合题意,舍去.
当![]() 时,D点坐标为(2,-2);
时,D点坐标为(2,-2);
综上所述,D点坐标为(6,10)或(2,-2).
(3)当BC为斜边构成Rt△BCD时,如下图所示,以BC中点O'为圆心,以BC为直径画圆,与抛物线交于D和D',
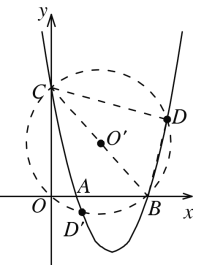
∵BC为圆O'的直径,
∴∠BDC=∠BD'C=90°,
∵![]() ,
,
∴D到O'的距离为圆O'的半径![]() ,
,
∵D点横坐标为m,纵坐标为![]() ,O'点坐标为(2,2),
,O'点坐标为(2,2),
∴![]()
即![]()
化简得:![]()
由图像易得m=0或4为方程的解,则方程左边必有因式![]() ,
,
∴采用因式分解法进行降次解方程
![]()
![]() 或
或![]() 或
或![]() ,
,
解得![]() ,
,![]() ,
,![]() ,
,![]()
当![]() 时,D点坐标为(0,4),与C点重合,舍去;
时,D点坐标为(0,4),与C点重合,舍去;
当![]() 时,D点坐标为(4,0),与B点重合,舍去;
时,D点坐标为(4,0),与B点重合,舍去;
当![]() 时,D点横坐标
时,D点横坐标![]() ;
;
当![]() 时,D点横坐标为
时,D点横坐标为![]() ;
;
结合(2)中△BCD形成直角三角形的情况,
可得△BCD为锐角三角形时,D点横坐标m的取值范围为3+![]() <m <6或 3-
<m <6或 3-![]() <m <2.
<m <2.


科目:初中数学 来源: 题型:
【题目】如图①,等边三角形![]() 的边长为2,
的边长为2,![]() 是
是![]() 边上的任一点(与
边上的任一点(与![]() 不重合),设
不重合),设![]() ,连接
,连接![]() ,以
,以![]() 为边向两侧作等边三角形
为边向两侧作等边三角形![]() 和等边三角形
和等边三角形![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)求四边形![]() 与△ABC重叠部分的面积
与△ABC重叠部分的面积![]() 与
与![]() 之间的函数关系式及
之间的函数关系式及![]() 的最小值;
的最小值;
(3)如图②,连接![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .当
.当![]() 为何值时,
为何值时,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
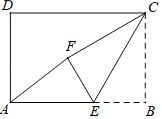
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD中,AB=AD,∠BAD=60°,边BC绕点B顺时针旋转120°得到BE,边DC绕点D逆时针旋转120°得到DF,四边形ABEG和四边形ADFH为平行四边形.
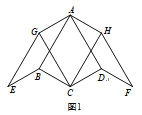
(1)如图1,若BC=CD,∠BCD=120°,则∠GCH=_______°;
(2)如图2,若BC≠CD,探究∠GCH的大小是否发生变化,并证明你的结论;
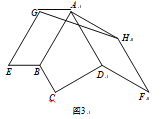
(3)如图3,若∠BCD=∠ADC=90°,AB=![]() 请直接写出△AGH的周长.
请直接写出△AGH的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
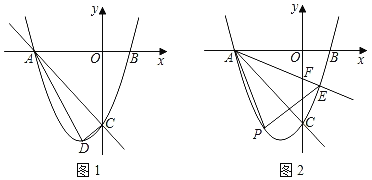
【题目】如图1,抛物线y=ax2+2ax+c(a≠0)与x轴交于点A,B(1,0)两点,与y轴交于点C,且OA=OC.
(1)求抛物线的解析式;
(2)点D是抛物线顶点,求△ACD的面积;
(3)如图2,射线AE交抛物线于点E,交y轴的负半轴于点F(点F在线段AE上),点P是直线AE下方抛物线上的一点,S△ABE=![]() ,求△APE面积的最大值和此动点P的坐标.
,求△APE面积的最大值和此动点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,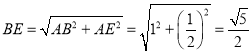 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
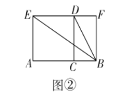
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
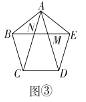
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com