
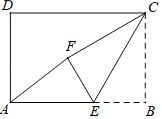
【题目】如图,在矩形ABCD中,AB=3,CB=2,点E为线段AB上的动点,将△CBE沿CE折叠,使点B落在矩形内点F处,下列结论正确的是_____(写出所有正确结论的序号)
①当E为线段AB中点时,AF∥CE;
②当E为线段AB中点时,AF=![]() ;
;
③当A、F、C三点共线时,AE=![]() ;
;
④当A、F、C三点共线时,△CEF≌△AEF.
【答案】①②③
【解析】分两种情形分别求解即可解决问题;
如图1中,当AE=EB时,
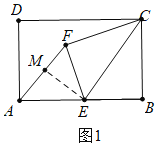
∵AE=EB=EF,
∴∠EAF=∠EFA,
∵∠CEF=∠CEB,∠BEF=∠EAF+∠EFA,
∴∠BEC=∠EAF,
∴AF∥EC,故①正确,
作EM⊥AF,则AM=FM,
在Rt△ECB中,EC=![]() ,
,
∵∠AME=∠B=90°,∠EAM=∠CEB,
∴△CEB∽△EAM,
∴![]() ,
,
∴![]() ,
,
∴AM=![]() ,
,
∴AF=2AM=![]() ,故②正确,
,故②正确,
如图2中,当A、F、C共线时,设AE=x.
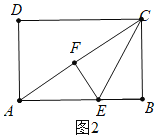
则EB=EF=3-x,AF=![]() -2,
-2,
在Rt△AEF中,∵AE2=AF2+EF2,
∴x2=(![]() -2)2+(3-x)2,
-2)2+(3-x)2,
∴x=![]() ,
,
∴AE=![]() ,故③正确,
,故③正确,
如果,△CEF≌△AEF,则∠EAF=∠ECF=∠ECB=30°,显然不符合题意,故④错误,
故答案为①②③.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】七年级同学最喜欢看哪一类课外书?某校随机抽取七年级部分同学对此进行问卷调査(每人只选择一种最喜欢的书籍类型).如图是根据调查结果绘制的两幅统计图(不完整).请根据统计图信息,解答下列问题:

(1)一共有多少名学生参与了本次问卷调查;
(2)补全条形统计图,并求出扇形统计图中“其他”所在扇形的圆心角度数;
(3)若该年级有400名学生,请你估计该年级喜欢“科普常识”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则![]() (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
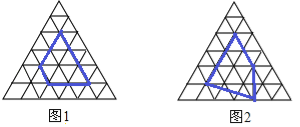
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图1,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,易知
,易知![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() .
.
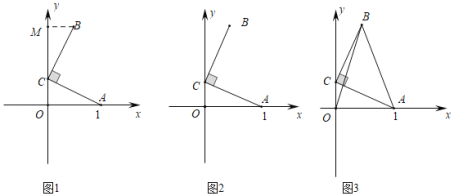
(探究)如图2,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() .
.
(1)求点![]() 的坐标.(用含
的坐标.(用含![]() 的代数式表示)
的代数式表示)
(2)求出BC所在直线的函数表达式.
(拓展)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,将线段
轴上,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
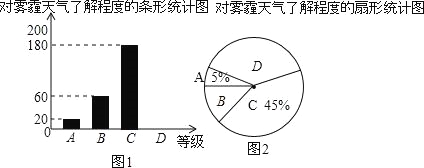
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
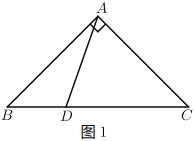
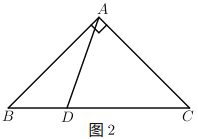
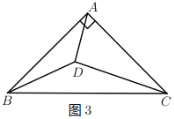
【题目】在![]() 中,
中,![]() ,
,![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
(2)如图2,若![]() 为线段
为线段![]() 上任意一点,探究
上任意一点,探究![]() ,
,![]() ,
,![]() 三者之间的关系,并证明.
三者之间的关系,并证明.
(3)如图3,若![]() ,
,![]() 为
为![]() 内一点,求
内一点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
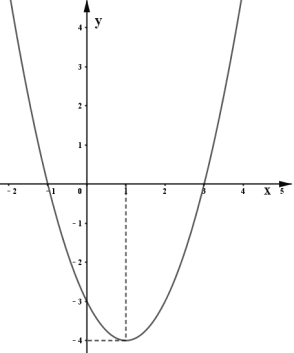
【题目】抛物线y=ax2+bx+c的图象如图所示,根据图象回答问题.
(1)直接写出x满足什么条件时,y随x的增大而增大;
(2)直接写出方程ax2+bx+c=0的根;
(3)直接写出不等式ax2+bx+c<0 的解集;
(4)若方程ax2+bx+c+k=1没有实数根,直接写出k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=x2+bx+c的图像与x轴交于A,B两点,B点坐标为(4,0),与y轴交于点C(0,4).点D为抛物线上一点
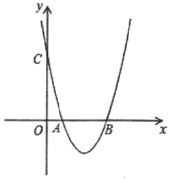
(1)求抛物线的解析式及A点坐标;
(2)若△BCD是以BC为直角边的直角三角形时,求点D的坐标;
(3)若△BCD是锐角三角形,请直接写出点D的横坐标m的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
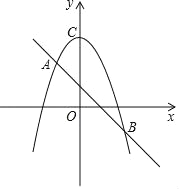
【题目】如图,一次函数y=kx+b的图象与二次函数y=﹣x2+c的图象相交于A(﹣1,2),B(2,n)两点.
(1)求一次函数和二次函数的解析式;
(2)根据图象直接写出使二次函数的值大于一次函数的值的x的取值范围;
(3)设二次函数y=﹣x2+c的图象与y轴相交于点C,连接AC,BC,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com