
ЁОЬтФПЁПгУЫЎЦНЯпКЭЪњЦ№ЯпНЋЦНУцЗжГЩШєИЩИіБпГЄЮЊ1ЕФаЁе§ЗНаЮИёзгЃЌаЁе§ЗНаЮЕФЖЅЕуГЦЮЊИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФЖрБпаЮГЦЮЊИёЕуЖрБпаЮЃЎЩшИёЕуЖрБпаЮЕФУцЛ§ЮЊSЃЌИУЖрБпаЮИїБпЩЯЕФИёЕуИіЪ§КЭЮЊaЃЌФкВПЕФИёЕуИіЪ§ЮЊbЃЌдђ![]() ЃЈЪЗГЦЁАЦЄПЫЙЋЪНЁБЃЉЃЎ
ЃЈЪЗГЦЁАЦЄПЫЙЋЪНЁБЃЉЃЎ
аЁУїШЯецбаОПСЫЁАЦЄПЫЙЋЪНЁБЃЌВЂЪмДЫЦєЗЂЖде§Ш§НЧПЊаЮЭјИёжаЕФРрЫЦЮЪЬтНјааЬНОПЃКе§Ш§НЧаЮЭјИёжаУПИіаЁе§Ш§НЧаЮУцЛ§ЮЊ1ЃЌаЁе§Ш§НЧаЮЕФЖЅЕуЮЊИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФЖрБпаЮГЦЮЊИёЕуЖрБпаЮЃЌЯТЭМЪЧИУе§Ш§НЧаЮИёЕу
жаЕФСНИіЖрБпаЮЃК
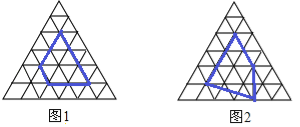
ИљОнЭМжаЬсЙЉЕФаХЯЂЬюБэЃК
ИёЕуЖрБпаЮИїБпЩЯЕФИёЕуЕФИіЪ§ | ИёЕуБпЖрБпаЮФкВПЕФИёЕуИіЪ§ | ИёЕуЖрБпаЮЕФУцЛ§ | |
ЖрБпаЮ1 | 8 | 1 | |
ЖрБпаЮ2 | 7 | 3 | |
Ё | Ё | Ё | Ё |
вЛАуИёЕуЖрБпаЮ | a | b | S |
дђSгыaЁЂbжЎМфЕФЙиЯЕЮЊS=ЁЁ ЁЁЃЈгУКЌaЁЂbЕФДњЪ§ЪНБэЪОЃЉЃЎ
 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
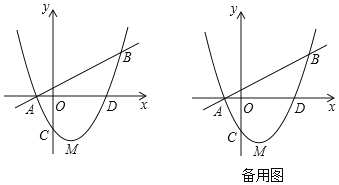
ЁОЬтФПЁПШчЭМвбжЊжБЯп![]() гыХзЮяЯпy=ax2+bx+cЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌmЃЉСНЕуЃЌХзЮяЯпy=ax2+bx+cНЛyжсгкЕуCЃЈ0ЃЌЉ
гыХзЮяЯпy=ax2+bx+cЯрНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌmЃЉСНЕуЃЌХзЮяЯпy=ax2+bx+cНЛyжсгкЕуCЃЈ0ЃЌЉ![]() ЃЉЃЌНЛxжсе§АыжсгкDЕуЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЎ
ЃЉЃЌНЛxжсе§АыжсгкDЕуЃЌХзЮяЯпЕФЖЅЕуЮЊMЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуPЮЊжБЯпABЯТЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌЕБЁїPABЕФУцЛ§зюДѓЪБЃЌЧѓЁїPABЕФУцЛ§МАЕуPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуQЮЊxжсЩЯвЛЖЏЕуЃЌЕуNдкХзЮяЯпЩЯЧвЮЛгкЦфЖдГЦжсгвВрЃЌЕБЁїQMNгыЁїMADЯрЫЦЪБЃЌЧѓNЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ФкНггкЁб
ФкНггкЁб![]() ЃЌЕу
ЃЌЕу![]() дк
дк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїЁб
зїЁб![]() ЕФЧаЯпЃЌЗжБ№НЛ
ЕФЧаЯпЃЌЗжБ№НЛ![]() ЃЌ
ЃЌ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
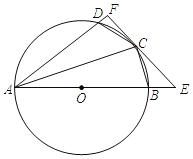
ЁОЬтФПЁПШчЭМЂйЃЌЕШБпШ§НЧаЮ![]() ЕФБпГЄЮЊ2ЃЌ
ЕФБпГЄЮЊ2ЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯЕФШЮвЛЕу(гы
БпЩЯЕФШЮвЛЕу(гы![]() ВЛжиКЯ)ЃЌЩш
ВЛжиКЯ)ЃЌЩш![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌвд
ЃЌвд![]() ЮЊБпЯђСНВрзїЕШБпШ§НЧаЮ
ЮЊБпЯђСНВрзїЕШБпШ§НЧаЮ![]() КЭЕШБпШ§НЧаЮ
КЭЕШБпШ§НЧаЮ![]() ЃЌЗжБ№гыБп
ЃЌЗжБ№гыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
(1)ЧѓжЄЃК![]() ЃЛ
ЃЛ
(2)ЧѓЫФБпаЮ![]() гыЁїABCжиЕўВПЗжЕФУцЛ§
гыЁїABCжиЕўВПЗжЕФУцЛ§![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНМА
жЎМфЕФКЏЪ§ЙиЯЕЪНМА![]() ЕФзюаЁжЕЃЛ
ЕФзюаЁжЕЃЛ
(3)ШчЭМЂкЃЌСЌНг![]() ЃЌЗжБ№гыБп
ЃЌЗжБ№гыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЎЕБ
ЃЎЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЃЎ
ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБЪжБЕФКЃАЖЯпЩЯвРДЮгаAЃЌBЃЌCШ§ИіИлПкЃЌМзДЌДгAИлПкГіЗЂЃЌбиКЃАЖЯпдШЫйЪЛЯђCИлПкЃЌ1аЁЪБКѓввДЌДгBИлПкГіЗЂЃЌбиКЃАЖЯпдШЫйЪЛЯђAИлПкЃЌСНДЌЭЌЪБЕНДяФПЕФЕиЃЎМзДЌЕФЫйЖШЪЧввДЌЕФ1.25БЖЃЌМзЁЂввСНДЌгыBИлПкЕФОрРыyЃЈkmЃЉгыМзДЌааЪЛЪБМфxЃЈhЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃЎИјГіЯТСаЫЕЗЈЃКЂйAЃЌBИлПкЯрОр400kmЃЛЂкМзДЌЕФЫйЖШЮЊ100km/hЃЛЂлBЃЌCИлПкЯрОр200kmЃЛЂмввДЌГіЗЂ4hЪБЃЌСНДЌЯрОр220kmЃЎЦфжае§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
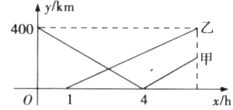
A.4B.3C.2D.1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
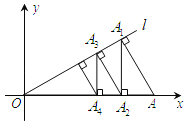
ЁОЬтФПЁПШчЭМЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЕФДЙЯпЃЌДЙзуЮЊЕу
ЕФДЙЯпЃЌДЙзуЮЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() жсЃЌДЙзуЮЊЕу
жсЃЌДЙзуЮЊЕу![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊЕу
ЃЌДЙзуЮЊЕу![]() ЁЃЌетбљвРДЮЯТШЅЃЌЕУЕНвЛзщЯпЖЮ
ЁЃЌетбљвРДЮЯТШЅЃЌЕУЕНвЛзщЯпЖЮ![]() ЁЃЌдђЯпЖЮ
ЁЃЌдђЯпЖЮ![]() ЕФГЄЮЊ__________ЃЎ
ЕФГЄЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() ЃК
ЃК![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЧвгыХзЮяЯпНЛгк
ЃЌЧвгыХзЮяЯпНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌ
СНЕуЃЌ![]() ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгы
ЮЊХзЮяЯпЩЯвЛЖЏЕуЃЈВЛгы![]() ЃЌ
ЃЌ![]() жиКЯЃЉ.
жиКЯЃЉ.
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕБЕу![]() дкжБЯп
дкжБЯп![]() ЯТЗНЪБЃЌЙ§Еу
ЯТЗНЪБЃЌЙ§Еу![]() зї
зї![]() жсНЛ
жсНЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() жсНЛ
жсНЛ![]() гкЕу
гкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ЃЈ3ЃЉЩш![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯЕФЕуЃЌвд
ЩЯЕФЕуЃЌвд![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЖЅЕуЕФЫФБпаЮФмЗёЙЙГЩЦНааЫФБпаЮЃПШєФмЃЌЧѓГіЕу
ЮЊЖЅЕуЕФЫФБпаЮФмЗёЙЙГЩЦНааЫФБпаЮЃПШєФмЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.
ЕФзјБъЃЛШєВЛФмЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
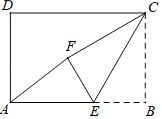
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=3ЃЌCB=2ЃЌЕуEЮЊЯпЖЮABЩЯЕФЖЏЕуЃЌНЋЁїCBEбиCEелЕўЃЌЪЙЕуBТфдкОиаЮФкЕуFДІЃЌЯТСаНсТле§ШЗЕФЪЧ_____ЃЈаДГіЫљгае§ШЗНсТлЕФађКХЃЉ
ЂйЕБEЮЊЯпЖЮABжаЕуЪБЃЌAFЁЮCEЃЛ
ЂкЕБEЮЊЯпЖЮABжаЕуЪБЃЌAF=![]() ЃЛ
ЃЛ
ЂлЕБAЁЂFЁЂCШ§ЕуЙВЯпЪБЃЌAE=![]() ЃЛ
ЃЛ
ЂмЕБAЁЂFЁЂCШ§ЕуЙВЯпЪБЃЌЁїCEFЁеЁїAEFЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНax2+2ax+cЃЈaЁй0ЃЉгыxжсНЛгкЕуAЃЌBЃЈ1ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЧвOAЃНOCЃЎ
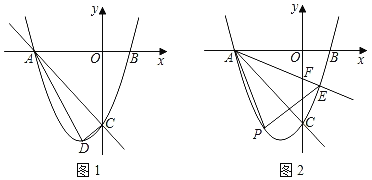
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуDЪЧХзЮяЯпЖЅЕуЃЌЧѓЁїACDЕФУцЛ§ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩфЯпAEНЛХзЮяЯпгкЕуEЃЌНЛyжсЕФИКАыжсгкЕуFЃЈЕуFдкЯпЖЮAEЩЯЃЉЃЌЕуPЪЧжБЯпAEЯТЗНХзЮяЯпЩЯЕФвЛЕуЃЌSЁїABEЃН![]() ЃЌЧѓЁїAPEУцЛ§ЕФзюДѓжЕКЭДЫЖЏЕуPЕФзјБъЃЎ
ЃЌЧѓЁїAPEУцЛ§ЕФзюДѓжЕКЭДЫЖЏЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com