
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,
两点,![]() 为抛物线上一动点(不与
为抛物线上一动点(不与![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,过点
下方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;(3)能,点
;(3)能,点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.
【解析】
(1)把B(3,0),C(0,2)代入![]() 解方程组即可得到结论;
解方程组即可得到结论;
(2)设P(m,![]() ),得到N(m,
),得到N(m,![]() ),
),![]() ,由两点间的距离公式得到关于m的二次函数,根据二次函数的性质即可得到结论;
,由两点间的距离公式得到关于m的二次函数,根据二次函数的性质即可得到结论;
(3)求得E(0,![]() ),得到CE=
),得到CE=![]() ,设P(m,
,设P(m,![]() ),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,
),①以CE为边,根据CE=PF,列方程得到m=1,m=0(舍去),②以CE为对角线,连接PF交CE于G,CG=GE,PG=FG,得到G(0,![]() ),设P(m,
),设P(m,![]() ),则F(m,
),则F(m,![]() ),列方程得到此方程无实数根,于是得到结论.
),列方程得到此方程无实数根,于是得到结论.
解:(1)把![]() ,
,![]() 代入
代入![]() 得
得 ,
,
∴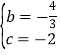 .
.
∴抛物线的解析式为:![]() .
.
(2)设![]() ,
,
∵![]() 轴,
轴,![]() 轴,
轴,![]() ,
,![]() 在直线
在直线![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]()
![]() ,
,
∴当![]() 时,
时,![]() 的最大值是
的最大值是![]() ;
;
(3)能,
理由:∵![]() 交y轴于点E,
交y轴于点E,
∴E(0,![]() ),
),
∴CE=![]() ,
,
设P(m,![]() ),
),
若以E,C,P,F为顶点的四边形能构成平行四边形,
①以CE为边,∴CE∥PF,CE=PF,
∴F(m,![]() ),
),
∴![]() 或
或![]() ,
,
∴m1=1,m2=0(舍去),m3=![]() ,m4=
,m4=![]() ,
,
∴F1(1,![]() ),F2(
),F2(![]() ),F3(
),F3(![]() ),
),
②以CE为对角线,连接PF交CE于G,
∴CG=GE,PG=FG,
∴G(0,![]() ),
),
设P(m,![]() ),则F(m,
),则F(m,![]() ),
),
∴![]() ×(
×(![]() ,
,
∴m=1,m=0(舍去),
F4(1,0),
综上所述点![]() 的坐标为
的坐标为![]() ,
,![]() ,
,![]() 或
或![]() .
.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:
【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,连接
,连接![]() ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点(
上的一个动点(![]() 不与
不与![]() ,
,![]() 两点重合),过点
两点重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]()
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则![]() (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
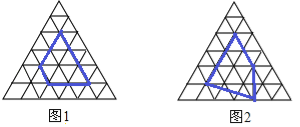
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了实现2020年全面脱贫目标,实施“精准扶贫”战略,采取异地搬迁,产业扶持等措施,使贫困户的生活条件得到改善,生活质量明显提高。某旗县为了解贫困县对扶贫工作的满意度情况,进行随机抽样调查,分四个类别A、非常满意;B、满意;C、基本满意;D、不满意.依据调查数据绘制成条形统计图和扇形统计图(不完整).根据以上信息,解答下列问题:
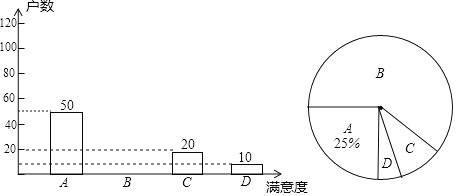
(1)D类别在扇形统计图中对应的圆心角度数是 ;
(2)将条形统计图补充完整;
(3)市扶贫办从该旗县甲乡镇3户和乙乡镇2户共5户贫困户中,随机抽取两户进行满意度回访,求这两户贫困户恰好都是同一乡镇的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(感知)如图1,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,易知
,易知![]() ,得到点
,得到点![]() 的坐标为
的坐标为![]() .
.
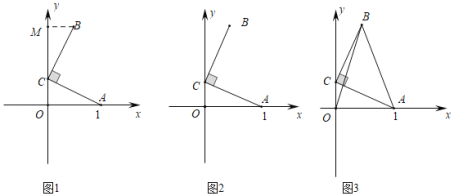
(探究)如图2,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() .
.
(1)求点![]() 的坐标.(用含
的坐标.(用含![]() 的代数式表示)
的代数式表示)
(2)求出BC所在直线的函数表达式.
(拓展)如图3,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 在
在![]() 轴上,将线段
轴上,将线段![]() 绕着点
绕着点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 至线段
至线段![]() ,连结
,连结![]() 、
、![]() ,则
,则![]() 的最小值为_______.
的最小值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点,某校学生会为了调查学生对雾霾天气知识的了解程度,随机抽取了该校的n名学生做了一次跟踪调查,将调查结果分为四个等级:(A)非常了解.(B)比较了解.(C)基本了解.(D)不了解,并将调查结果绘制成如下两幅不完整统计图.
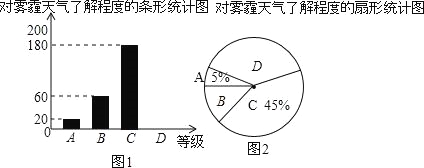
根据统计图提供的信息,解答下列问题:
(1)求n的值;
(2)在调查的n名学生中,对雾霾天气知识不了解的学生有 人,并将条形统计图补充完整.
(3)估计该校1500名学生中,对雾霾天气知识比较了解的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
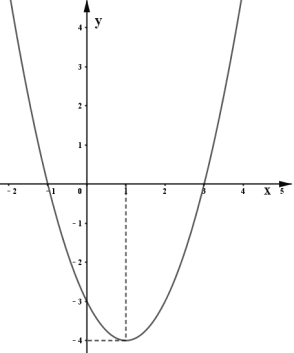
【题目】抛物线y=ax2+bx+c的图象如图所示,根据图象回答问题.
(1)直接写出x满足什么条件时,y随x的增大而增大;
(2)直接写出方程ax2+bx+c=0的根;
(3)直接写出不等式ax2+bx+c<0 的解集;
(4)若方程ax2+bx+c+k=1没有实数根,直接写出k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com