
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,连接
,连接![]() ,与抛物线的对称轴交于点
,与抛物线的对称轴交于点![]() ,点
,点![]() 为线段
为线段![]() 上的一个动点(
上的一个动点(![]() 不与
不与![]() ,
,![]() 两点重合),过点
两点重合),过点![]() 作
作![]() 轴的垂线交抛物线于点
轴的垂线交抛物线于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]()
(1)当![]() 为何值时,四边形
为何值时,四边形![]() 为平行四边形;
为平行四边形;
(2)设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值.
的最大值.

【答案】(1)当![]() 时,四边形
时,四边形![]() 为平行四边形;(2)
为平行四边形;(2)![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)对于抛物线解析式,令x=0求出y的值确定出C的坐标,令y=0求出x的值,确定出A与B坐标,根据B与C坐标,利用待定系数法确定出直线BC解析式,进而表示出E与P坐标,根据抛物线解析式确定出D与F坐标,表示出PF,利用平行四边形的判定方法确定出m的值即可;
(2)先求出OB的长,△BCF面积![]() ,列出S关于m的二次函数解析式,利用二次函数性质确定出S的最大值即可.
,列出S关于m的二次函数解析式,利用二次函数性质确定出S的最大值即可.
(1)对于抛物线![]() ,
,
![]() 顶点
顶点![]()
令![]() ,得到
,得到![]() ;
;
令![]() ,得到
,得到![]() ,即
,即![]() ,
,
解得:![]() 或
或![]() ,
,
则![]() ,
,![]() ,
,![]() ,抛物线对称轴为直线
,抛物线对称轴为直线![]() ;
;
设直线![]() 的函数解析式为
的函数解析式为![]() ,
,
把![]() ,
,![]() 分别代入得:
分别代入得:![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() 线段
线段![]() ,
,
连接![]() ,由
,由![]() ,得到当
,得到当![]() 时,四边形
时,四边形![]() 为平行四边形,
为平行四边形,
由![]() ,得到
,得到![]() 或
或![]() (不合题意,舍去),
(不合题意,舍去),
当![]() 时,四边形
时,四边形![]() 为平行四边形;
为平行四边形;
(2)![]() ,
,
![]() ,
,
![]() ,
,
则当![]() 时,
时,![]() 取得最大值为
取得最大值为![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )
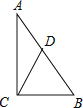
A.∠A+∠DCB=90°B.∠ADC= 2∠BC. AB=2CDD. BC=CD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要将一份宣传资料进行批量印刷.在甲印刷厂,在收取100元制版费的基础上,每份收费0.5元;在乙印刷厂,在收取40元侧版费的基础上,每份收费0.7元.设该单位要印刷此宣传资料![]() 份(
份(![]() 为正整数).
为正整数).
(Ⅰ)根据题意,填写下表:
印剧数量(份) | 150 | 250 | 350 | 450 | … |
甲印刷厂收费(元) | 175 | ① | 275 | ② | … |
乙印刷厂收费(元) | 145 | 215 | ③ | 355 | … |
(Ⅱ)设在甲印刷厂收费![]() 元,在乙印刷厂收费
元,在乙印刷厂收费![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(Ⅲ)当![]() 时,在哪家印刷厂花费少?请说明理由.
时,在哪家印刷厂花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
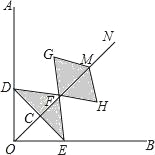
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,等边三角形![]() 的边长为2,
的边长为2,![]() 是
是![]() 边上的任一点(与
边上的任一点(与![]() 不重合),设
不重合),设![]() ,连接
,连接![]() ,以
,以![]() 为边向两侧作等边三角形
为边向两侧作等边三角形![]() 和等边三角形
和等边三角形![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)求四边形![]() 与△ABC重叠部分的面积
与△ABC重叠部分的面积![]() 与
与![]() 之间的函数关系式及
之间的函数关系式及![]() 的最小值;
的最小值;
(3)如图②,连接![]() ,分别与边
,分别与边![]() 交于点
交于点![]() .当
.当![]() 为何值时,
为何值时,![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】笔直的海岸线上依次有A,B,C三个港口,甲船从A港口出发,沿海岸线匀速驶向C港口,1小时后乙船从B港口出发,沿海岸线匀速驶向A港口,两船同时到达目的地.甲船的速度是乙船的1.25倍,甲、乙两船与B港口的距离y(km)与甲船行驶时间x(h)之间的函数关系如图所示.给出下列说法:①A,B港口相距400km;②甲船的速度为100km/h;③B,C港口相距200km;④乙船出发4h时,两船相距220km.其中正确的个数是( )
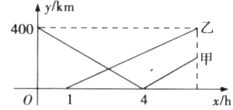
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,直线
,直线![]() :
:![]() 交
交![]() 轴于点
轴于点![]() ,且与抛物线交于
,且与抛物线交于![]() ,
,![]() 两点,
两点,![]() 为抛物线上一动点(不与
为抛物线上一动点(不与![]() ,
,![]() 重合).
重合).
(1)求抛物线的解析式;
(2)当点![]() 在直线
在直线![]() 下方时,过点
下方时,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,
,![]() 轴交
轴交![]() 于点
于点![]() ,求
,求![]() 的最大值.
的最大值.
(3)设![]() 为直线
为直线![]() 上的点,以
上的点,以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形能否构成平行四边形?若能,求出点
为顶点的四边形能否构成平行四边形?若能,求出点![]() 的坐标;若不能,请说明理由.
的坐标;若不能,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com