
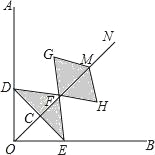
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠无缝隙地放在一个底面为矩形(长为15cm,宽为12cm)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
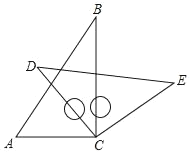
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(x<0)的图象相交于点A、点B,与X轴交于点C,其中点A(﹣1,3)和点B(﹣3,n).
(1)填空:m= ,n= .
(2)求一次函数的解析式和△AOB的面积.
(3)根据图象回答:当x为何值时,kx+b≥![]() (请直接写出答案) .
(请直接写出答案) .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a,b,定义一种新运算“⊙”,规定a⊙b=|a+b|+|a﹣b|.
![]()
(1)计算2⊙(﹣3)的值;
(2)当a,b在数轴上的位置如图所示时,化简a⊙b;
(3)已知(a⊙a)⊙a=8+a,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在等边三角形ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).

(1)连接EF,当EF经过AC边的中点D时,求证:四边形AFCE是平行四边形;
(2)填空:①当t为 s时,四边形ACFE是菱形;②当t为 s时,△ACE的面积是△ACF的面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”。图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位,动点P从点A出发,以2单位/秒的速度沿着“折线数轴”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位/秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速,设运动的时间为t秒,问:
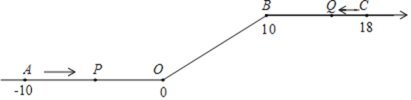
(1)动点P从点A运动至点C需要________秒;
(2)P、Q两点相遇时,求出相遇点M所对应的数是多少?
(3)求当t为何值时,P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元![]() 的价格进了同样的60包茶叶,如果商家以每包
的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这些茶叶,卖完后,这家商店( )
元的价格卖出这些茶叶,卖完后,这家商店( )
A. 盈利了B. 亏损了C. 不盈不亏D. 盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
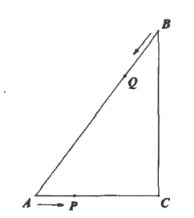
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com