
����Ŀ����ͼ����һ��������ԭ��O�͵�B������һ�£��õ�һ����������������ͼ�е�A��ʾ-10����B��ʾ10����C��ʾ18�����dzƵ�A�͵�C�����������28�����ȵ�λ������P�ӵ�A��������2��λ/����ٶ��������������������������˶����ӵ�O�˶�����B�ڼ��ٶȱ�Ϊԭ����һ�룬֮�����ָ̻�ԭ�٣�ͬʱ������Q�ӵ�C��������1��λ/����ٶ���������ĸ������˶����ӵ�B�˶�����O�ڼ��ٶȱ�Ϊԭ����������֮��Ҳ���ָ̻�ԭ�٣����˶���ʱ��Ϊt�룬�ʣ�
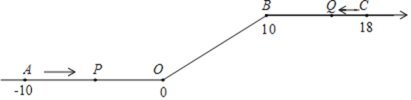
��1������P�ӵ�A�˶�����C��Ҫ________�룻
��2��P��Q��������ʱ�����������M����Ӧ�����Ƕ��٣�
��3����tΪ��ֵʱ��P��O���������������ij�����Q��B���������������ij������.
���𰸡���1��19�룻��2��������M����Ӧ������![]() ����3��t��ֵΪ2��6.5��11��17
����3��t��ֵΪ2��6.5��11��17
��������
��1������·�̳����ٶȵ���ʱ�䣬�ɵô𰸣�
��2����������ʱP��Q�˶���ʱ����ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
��3������PO��BQ��ȣ��ɵ÷��̣��ⷽ�̣��ɵô𰸣�
�⣺��1����P�˶�����Cʱ������ʱ��t=![]() ���룩��
���룩��
��2�������֪��P��Q�����������߶�OB����M������OM=![]() ��
��
��![]() ��
��
���![]() ����������M����Ӧ������
����������M����Ӧ������![]() ��
��
��3��P��O���������������ij�����Q��B���������������ij��������4�ֿ��ܣ�
�ٶ���Q��CB�ϣ�����P��AO�ϣ���8-t=10-2t����ã�t=2��
�ڶ���Q��CB�ϣ�����P��OB�ϣ���8-t=��t-5����1����ã�t=6.5��
�۶���Q��BO�ϣ�����P��OB�ϣ���2��t-8��=��t-5����1����ã�t=11��
�ܶ���Q��OA�ϣ�����P��BC�ϣ���10+2��t-15��=t-13+10����ã�t=17��
����������t��ֵΪ2��6.5��11��17��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c���㣺 (1)5(a+3)+2|b2|=0�� (2)![]() x
x![]() y
y![]() +2a
+2a![]() b+c+1���ߴζ���ʽ��
b+c+1���ߴζ���ʽ��
�����ʽab[ab(2abcac3ab)4ac]abc��ֵ..
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и��������ʾ�����ڵ�������������
������2.3����![]() ��0����
��0����![]() ��30%��������|��2013|����5
��30%��������|��2013|����5![]() ��
��![]()
��1������������[�� ����]
��2��������������[�� ����]
��3����������[�� ����]
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��AOB��ƽ����ON������ȡ��C��F��M������C��DE��OC���ֱ�OA��OB�ڵ�D��E����FMΪ�Խ���������FGMH����֪��DFE=��GFH=120�㣬FG=FE����OC=x��ͼ����Ӱ�������Ϊy����y��x֮��ĺ�����ϵʽ�ǣ� ��
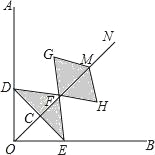
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪A��a2��2b2+2ab��3��B��2a2��b2��![]() ab��
ab��![]() ��
��
(1)��2(A+B)��3(2A��B)��ֵ(����û�����a��b��ʽ�ӱ�ʾ)��
(2)��![]() ��b2��Ϊ�෴��ʱ����(1)��ʽ�ӵ�ֵ��
��b2��Ϊ�෴��ʱ����(1)��ʽ�ӵ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
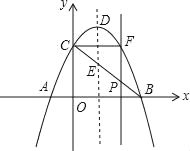
����Ŀ����ͼ��������y=��x2+2x+3��x�ύ��A��B���㣨��A�ڵ�B����ࣩ����y���ཻ�ڵ�C������ΪD������BC���������ߵĶԳ��ύ�ڵ�E����PΪ�߶�BC�ϵ�һ�����㣨P����B��C�����غϣ�������P��x��Ĵ��߽��������ڵ�F�����P�ĺ�����Ϊm��0��m��3��
��1����mΪ��ֵʱ���ı���PEDFΪƽ���ı��Σ�
��2�����BCF�����ΪS����S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʮһ���ƽ����ڼ�,ij�羰����7�������ÿ�����ε������仯���±�(������ʾ��ǰһ��������,������ʾ��ǰһ���ٵ�����,��λ:����),��֪9��30�յ��ο�����Ϊ0.3����,��ش���������:
�� �� | 1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
�����仯 | +1.8 | +0.8 | +0.2 | -0.4 | -0.8 | +0.2 | -1.0 |
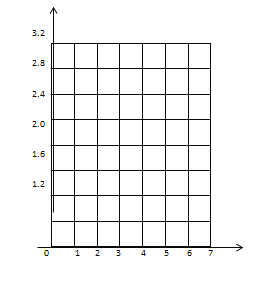
(1)�������ο����������� ��,���ٵ��� �գ�
(2)����9��30�յ��ο�����Ϊ0��,������ͳ��ͼ��ʾ��7����ο������仯���?
(3)����7����ο������Ƕ�������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ص�һ���˶����蹺��A��B���ֽ�Ʒ��������A�ֽ�Ʒ4����B�ֽ�Ʒ3��������85Ԫ��������A�ֽ�Ʒ3����B�ֽ�Ʒ1��������45Ԫ��
��1����A��B���ֽ�Ʒ�ĵ��۸��Ƕ���Ԫ��
��2���˶�����ί��ƻ�����A��B���ֽ�Ʒ��100����������ò�����1150Ԫ����A�ֽ�Ʒ������������B�ֽ�Ʒ������3�����蹺��A�ֽ�Ʒm���������ܷ���WԪ��д��W��Ԫ����m������֮��ĺ�����ϵʽ������Ա���m��ȡֵ��Χ������Ƴ������ܷ������ٵķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ� С����ѧϰ���θ�ʽ����һЩ�����ŵ�ʽ�ӿ���д����һ��ʽ�ӵ�ƽ�����磺![]() ������˼����С������������̽����
������˼����С������������̽����
��![]() ������
������![]() ��������������
��������������![]() ��
��
��![]() ������С�����ҵ���һ�ְѲ���
������С�����ҵ���һ�ְѲ���![]() ��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
��ʽ�ӻ�Ϊƽ��ʽ�ķ�����
�������С���ķ���̽��������������⣺
��![]() ��Ϊ������ʱ����
��Ϊ������ʱ����![]() ���ú�m��n��ʽ�ӷֱ��ʾ
���ú�m��n��ʽ�ӷֱ��ʾ![]() ����
����![]() ���� ����
���� ����![]() ���� ����
���� ����
��2��������̽���Ľ��ۣ���һ��������![]() ����գ� ���� ����(�� ������ ��
����գ� ���� ����(�� ������ ��![]() )2��
)2��
��3����![]() ����
����![]() ������������
��Ϊ����������![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com