
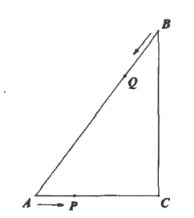
【题目】如图,已知![]() 中,
中,![]() ,点
,点![]() 以每秒1个单位的速度从
以每秒1个单位的速度从![]() 向
向![]() 运动,同时点
运动,同时点![]() 以每秒2个单位的速度从
以每秒2个单位的速度从![]() 向
向![]() 方向运动,
方向运动,![]() 到达
到达![]() 点后,
点后,![]() 点也停止运动,设点
点也停止运动,设点![]() 运动的时间为
运动的时间为![]() 秒.
秒.
(1)求![]() 点停止运动时,
点停止运动时,![]() 的长;
的长;
(2) ![]() 两点在运动过程中,点
两点在运动过程中,点![]() 是
是![]() 点关于直线
点关于直线![]() 的对称点,是否存在时间
的对称点,是否存在时间![]() ,使四边形
,使四边形![]() 为菱形?若存在,求出此时
为菱形?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(3) ![]() 两点在运动过程中,求使
两点在运动过程中,求使![]() 与
与![]() 相似的时间
相似的时间![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() 或
或![]()
【解析】
(1)求出点Q的从B到A的运动时间,再求出AP的长,利用勾股定理即可解决问题.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.根据DQ=CK,构建方程即可解决问题.
(3)分两种情形:如图3-1中,当∠APQ=90°时,如图3-2中,当∠AQP=90°时,分别构建方程即可解决问题.
(1)在Rt△ABC中,∵∠C=90°,AC=6,BC=8,
∴AB=![]() =10,
=10,
点Q运动到点A时,t=![]() =5,
=5,
∴AP=5,PC=1,
在Rt△PBC中,PB=![]() .
.
(2)如图1中,当四边形PQCE是菱形时,连接QE交AC于K,作QD⊥BC于D.
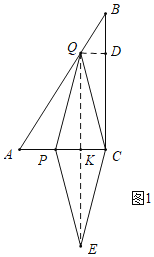
∵四边形PQCE是菱形,
∴PC⊥EQ,PK=KC,
∵∠QKC=∠QDC=∠DCK=90°,
∴四边形QDCK是矩形,
∴DQ=CK,
∴![]() ,
,
解得t=![]() .
.
∴t=![]() s时,四边形PQCE是菱形.
s时,四边形PQCE是菱形.
(3)如图2中,当∠APQ=90°时,
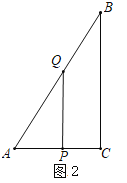
∵∠APQ=∠C=90°,
∴PQ∥BC,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
如图3中,当∠AQP=90°时,
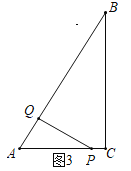
∵△AQP∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,![]() 或
或![]() s时,△APQ是直角三角形.
s时,△APQ是直角三角形.


科目:初中数学 来源: 题型:
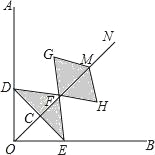
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县第一届运动会需购买A,B两种奖品,若购买A种奖品4件和B种奖品3件,共需85元;若购买A种奖品3件和B种奖品1件,共需45元.
(1)求A、B两种奖品的单价各是多少元?
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买总费用W元,写出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并设计出购买总费用最少的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
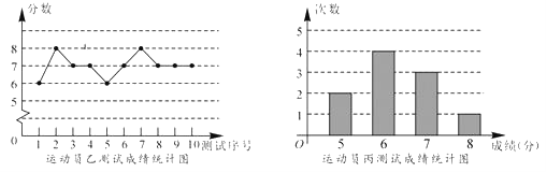
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
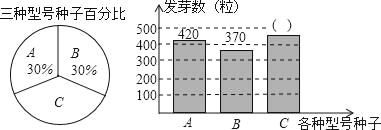
【题目】松山区种子培育基地用A,B,C三种型号的甜玉米种子共1500粒进行发芽试验,从中选出发芽率高的种子进行推广,通过试验知道,C型号种子的发芽率为80%,根据试验数据绘制了下面两个不完整的统计图:
(1)求C型号种子的发芽数;
(2)通过计算说明,应选哪种型号的种子进行推广?
(3)如果将所有已发芽的种子放在一起,从中随机取出一粒,求取到C型号发芽种子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上,一动点![]() 从原点
从原点![]() 出发,沿直线以每秒钟
出发,沿直线以每秒钟![]() 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度…
个单位长度…
![]()
(1)求出![]() 秒钟后动点
秒钟后动点![]() 所处的位置;
所处的位置;
(2)如果在数轴上还有一个定点![]() ,且
,且![]() 与原点
与原点![]() 相距20个单位长度,问:动点
相距20个单位长度,问:动点![]() 从原点出发,可能与点
从原点出发,可能与点![]() 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点![]() 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个式子的平方,如:![]() ,善于思考的小明进行了以下探索:
,善于思考的小明进行了以下探索:
设![]() (其中
(其中![]() 均为整数),则有
均为整数),则有![]() .
.
∴![]() .这样小明就找到了一种把部分
.这样小明就找到了一种把部分![]() 的式子化为平方式的方法.
的式子化为平方式的方法.
请你仿照小明的方法探索并解决下列问题:
当![]() 均为正整数时,若
均为正整数时,若![]() ,用含m、n的式子分别表示
,用含m、n的式子分别表示![]() ,得
,得![]() = ,
= ,![]() = ;
= ;
(2)利用所探索的结论,找一组正整数![]() ,填空: + =( +
,填空: + =( + ![]() )2;
)2;
(3)若![]() ,且
,且![]() 均为正整数,求
均为正整数,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(﹣3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交于y轴于点H.
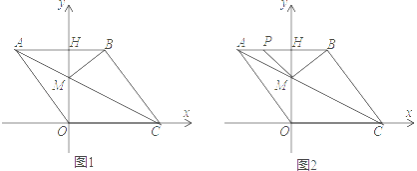
(1)连接BM,动点P从点A出发,沿折线ABC方向以1个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(2)在(1)的情况下,当点P在线段AB上运动时,是否存在以BM为腰的等腰三角形BMP?如存在,求出t的值;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
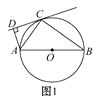
【题目】如图1,AB是☉O的直径,C为☉O上一点,直线CD与☉O相切于点C,AD⊥CD,垂足为D.
(1)求证:△ACD∽△ABC.
(2)如图2,将直线CD向下平移与☉O相交于点C,G,但其他条件不变.若AG=4,BG=3,求tan∠CAD的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com