
����Ŀ����֪�������ϣ�һ����![]() ��ԭ��
��ԭ��![]() ��������ֱ����ÿ����
��������ֱ����ÿ����![]() ����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�
����λ���ȵ��ٶ������ƶ������ƶ���ʽ���������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ���ȣ��������ƶ�
����λ���ȣ��������ƶ�![]() ����λ������
���������
![]()
��1�����![]() ���Ӻ�
���Ӻ�![]() ������λ�ã�
������λ�ã�
��2������������ϻ���һ������![]() ����
����![]() ��ԭ��
��ԭ��![]() ���20����λ���ȣ��ʣ�����
���20����λ���ȣ��ʣ�����![]() ��ԭ��������������
��ԭ��������������![]() �غ������ܣ����һ�����
�غ������ܣ����һ�����![]() �غ���ʱ�䣿�����ܣ���˵�����ɣ�
�غ���ʱ�䣿�����ܣ���˵�����ɣ�
���𰸡���1��Q���ک�2����2���ٵ���A��ԭ�����ʱ��ʱ��=390�루6.5���ӣ����ڵ���Aԭ�����ʱ��ʱ��=410�� ��6![]() ���ӣ���
���ӣ���
��������
��1���ȸ���·��=�ٶ���ʱ�����5�����߹���·�̣�Ȼ���������Ҽ���ʽ���㼴�ɵý⣻
��2���ֵ�A��ԭ��������ұ���������ֱ���������߹���·�̣�Ȼ�����ʱ��=·�����ٶȼ��㼴�ɵý⣮
�⣺��1����2��5=10��
����Q�߹���·����1+2+3+4=10��Q���ڣ�1��2+3��4=4��6=��2��
��2��������A��ԭ�����ʱ������Ҫ��n�ε����A����![]() =20�����n=39��
=20�����n=39��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+|��38|+39��
=1+2+3+��+39��
=![]() =780��
=780��
��ʱ��=780��2=390�루6.5���ӣ���
������Aԭ�����ʱ������Ҫ��n�ε����A����![]() =20��
=20��
���n=40��
������Q�߹���·����
1+|��2|+3+|��4|+5+��+39+|��40|��
=1+2+3+��+40��
=![]() =820��
=820��
��ʱ��=820��2=410�� ��6![]() ���ӣ���
���ӣ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڵȱ�������ABC�У�BC��8cm������AG��BC����E�ӵ�A����������AG��1cm/s���ٶ��˶���ͬʱ��F�ӵ�B����������BC��2cm/s���ٶ��˶������˶�ʱ��Ϊt��s����

��1������EF����EF����AC�ߵ��е�Dʱ����֤���ı���AFCE��ƽ���ı��Σ�
��2����գ��ٵ�tΪ�� ��sʱ���ı���ACFE�����Σ��ڵ�tΪ�� ��sʱ����ACE������ǡ�ACF�������2����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��ǽ��AOB��OA��OB����OA��OB���Ȳ��ޣ��У�Ҫ��20m����ǽ����ֱ��ǽ��AOBΧ�ɵ���Ϊ���εĴ��֣��ҵ������AOBC�����Ϊ96m2��
��1����������AOBC�ij���
��2���й��Ϊ0.80��0.80��1.00��1.00����λ��m���ĵذ�ש���۷ֱ�Ϊ55Ԫ/���80Ԫ/�飬��ֻѡ����һ�ֵذ�ש��ǡ�����������ֵľ��ε��棨���Ʒ�϶��������һ�ֹ��ĵذ�ש���ý��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
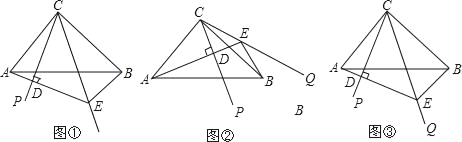
����Ŀ����ͼ������ABC�У���ACB=90����AC=BC����PCQ=45�����ѡ�PCQ�Ƶ�C��ת����������ת�����У�����A��AD��CP������ΪD��ֱ��AD��CQ��E��
��1����ͼ�٣�����PCQ�ڡ�ACB�ڲ�ʱ����֤��AD+BE=DE��
��2����ͼ�ڣ���CQ�ڡ�ACB�ⲿʱ�����߶�AD��BE��DE�Ĺ�ϵΪ_____��
��3���ڣ�1���������£���CD=6��S��BCE=2S��ACD����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪![]() �У�
��![]() ����
����![]() ��ÿ��1����λ���ٶȴ�
��ÿ��1����λ���ٶȴ�![]() ��
��![]() �˶���ͬʱ��
�˶���ͬʱ��![]() ��ÿ��2����λ���ٶȴ�
��ÿ��2����λ���ٶȴ�![]() ��
��![]() �����˶���
�����˶���![]() ����
����![]() ���
���![]() ��Ҳֹͣ�˶������
��Ҳֹͣ�˶������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ��.
��.
(1)��![]() ��ֹͣ�˶�ʱ��
��ֹͣ�˶�ʱ��![]() �ij�;
�ij�;
(2) ![]() �������˶������У���
�������˶������У���![]() ��
��![]() �����ֱ��
�����ֱ��![]() �ĶԳƵ㣬�Ƿ����ʱ��
�ĶԳƵ㣬�Ƿ����ʱ��![]() ��ʹ�ı���
��ʹ�ı���![]() Ϊ����?�����ڣ������ʱ
Ϊ����?�����ڣ������ʱ![]() ��ֵ;�������ڣ���˵������.
��ֵ;�������ڣ���˵������.
(3) ![]() �������˶������У���ʹ
�������˶������У���ʹ![]() ��
��![]() ���Ƶ�ʱ��
���Ƶ�ʱ��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,����ͼ�ζ��������Ϊ1�������ΰ�һ���Ĺ������,����,��(1)��ͼ�������Ϊ1����������2��,��(2)��ͼ�������Ϊ1����������5��,��(3)��ͼ�������Ϊ1����������9��,��,���˹��ɡ����(6)��ͼ�������Ϊ1�������εĸ���Ϊ()

A. 20B. 25C. 35D. 27
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A�����ƶ�1����λ�õ���B����B�����ƶ���n+1����nΪ������������λ�õ���C����A��B��C�ֱ��ʾ������a��b��c��
��1����n=1ʱ��
����A��B��C�����������ϵ�λ����ͼ��ʾ��a��b��c�������ij˻�Ϊ������������ԭ���λ�ÿ��� ��
A���ڵ�A������A��B����֮�� B���ڵ�C�Ҳ����A��B����֮��
C���ڵ�A������B��C����֮�� D���ڵ�C�Ҳ����B��C����֮��
�������������ĺ������е�һ������ȣ���a��ֵ��
��2������C�����ƶ���n+2������λ�õ���D����D��ʾ������d��a��b��c��d�ĸ����Ļ�Ϊ���������ĸ����ĺ������е��������ĺ���ȣ���aΪ���������������ϱ����D���ú�n�Ĵ���ʽ��ʾa��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1+2+22+23+��+22018��ֵ������S��1+2+22+23+��+22018����2S��2+22+23+24+��22019�����2S��S��22019��1����S��22019��1���������ϵķ����������1+5+52+53+��52017��ֵΪ��������
A. 52018��1 B. 52019��1 C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�����ϴ��������㣬����һ���������ٶȶ���Ϊԭ�����������ڶ����������ֶ��ָܻ���ԭ�����ٶȣ������������Ϊħ�����ᣮ
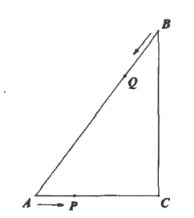
��ͼ����֪һħ����������A��O��B���㣬����A��O��Ӧ�����ֱ�Ϊ��10��0��ABΪ47����λ���ȣ��ף��ҷֱ��A��O����ͬʱ������������������ͬ����У����ٶ�Ϊ3����λ/�룬�ҵ��ٶ�Ϊ1����λ/�룬�����B���Ե�ʱ�ٶ��������أ����ص���Aʱ���ס���ͬʱֹͣ�˶���
![]()
�ʣ���1����B��Ӧ����Ϊ�� �����׳����� ��������ң�����һ��������
��2���������B�������غ�ڶ�����������������������������ϱ�ʾ�����Ƕ��٣�
��3���ס���ͬʱ����������������2����λ���ȣ�����ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com