
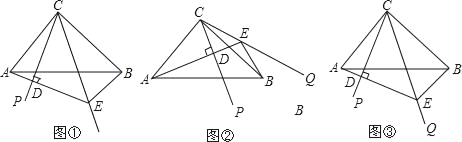
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.
【答案】(1)见解析 (2)AD=BE+DE (3)8
【解析】试题分析:(1)延长DA到F,使DF=DE,根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得证;
(2)在AD上截取DF=DE,然后根据线段垂直平分线上的点到线段两端点的距离相等可得CE=CF,再求出∠ACF=∠BCE,然后利用“边角边”证明△ACF和△BCE全等,根据全等三角形的即可证明AF=BE,从而得到AD=BE+DE;
(3)根据等腰直角三角形的性质求出CD=DF=DE,再根据等高的三角形的面积的比等于底边的比求出AF=2AD,然后求出AD的长,再根据AE=AD+DE代入数据进行计算即可得解.
试题解析:(1)证明:如图①,延长DA到F,使DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ACD+∠ACF=∠DCF=45°.又∵∠ACB=90°,∠PCQ=45°,∴∠ACD+∠BCE=90°﹣45°=45°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD+BE=AD+AF=DF=DE,即AD+BE=DE;
(2)解:如图②,在AD上截取DF=DE.∵CD⊥AE,∴CE=CF,∴∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=∠DCE+∠DCF=90°,∴∠BCE+∠BCF=∠ECF=90°.又∵∠ACB=90°,∴∠ACF+∠BCF=90°,∴∠ACF=∠BCE.在△ACF和△BCE中,∵ ,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
,∴△ACF≌△BCE(SAS),∴AF=BE,∴AD=AF+DF=BE+DE,即AD=BE+DE;
故答案为:AD=BE+DE.
(3)∵∠DCE=∠DCF=∠PCQ=45°,∴∠ECF=45°+45°=90°,∴△ECF是等腰直角三角形,∴CD=DF=DE=6.∵S△BCE=2S△ACD,∴AF=2AD,∴AD=![]() ×6=2,∴AE=AD+DE=2+6=8.
×6=2,∴AE=AD+DE=2+6=8.



 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】一病人发高烧进医院进行治疗,医生给他开了药并挂了水,同时护士每隔1小时对病人测体温,及时了解病人的好转情况,现护士对病人测体温的变化数据如下表:
时 间 | 7:00 | 8:00 | 9:00 | 10:00 | 11:00 | 12:00 | 13:00 | 14:00 | 15:00 |
体温 | 升0.2 | 降1.0 | 降0.8 | 降1.0 | 降0.6 | 升0.4 | 降0.2 | 降0.2 | 降0 |
注:病人早晨进院时医生测得病人体温是40.2℃。
问:(1)病人什么时候体温达到最高,最高体温是多少?
(2)病人中午12点时体温多高?
(3)病人几点后体温稳定正常?(正常体温是37℃)
查看答案和解析>>
科目:初中数学 来源: 题型:
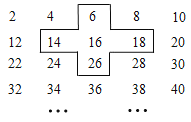
【题目】探索规律:将连续的偶数2,4,6,8,…,排成如表:
(1)十字框中的五个数的和与中间的数16有什么关系?
(2)移动十字框,设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其它五个数的和能等于2560吗?若能,写出这五个数,若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )

A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
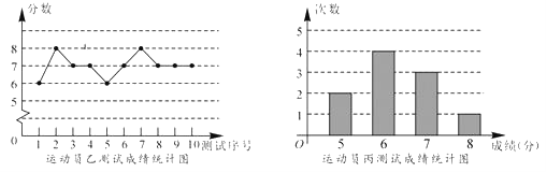
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上,一动点![]() 从原点
从原点![]() 出发,沿直线以每秒钟
出发,沿直线以每秒钟![]() 个单位长度的速度来回移动,其移动方式是先向右移动
个单位长度的速度来回移动,其移动方式是先向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度,再向左移动
个单位长度,再向左移动![]() 个单位长度,又向右移动
个单位长度,又向右移动![]() 个单位长度…
个单位长度…
![]()
(1)求出![]() 秒钟后动点
秒钟后动点![]() 所处的位置;
所处的位置;
(2)如果在数轴上还有一个定点![]() ,且
,且![]() 与原点
与原点![]() 相距20个单位长度,问:动点
相距20个单位长度,问:动点![]() 从原点出发,可能与点
从原点出发,可能与点![]() 重合吗?若能,则第一次与点
重合吗?若能,则第一次与点![]() 重合需多长时间?若不能,请说明理由.
重合需多长时间?若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定x的一元一次方程ax=b的解为b﹣a,则称该方程是“差解方程”,例如:3x=4.5的解为4.5﹣3=1.5,则该方程3x=4.5就是“差解方程”,请根据上述规定解答下列问题:
(1)已知关于x的一元一次方程4x=m是“差解方程”,则m=______.
(2)已知关于x的一元一次方程4x=ab+a是“差解方程”,它的解为a,则a+b=_____.
(3)已知关于x的一元一次方程4x=mn+m和﹣2x=mn+n都是“差解方程”,求代数式﹣3(m+11)+4n+2[(mn+m)2﹣m]﹣![]() [(mn+n)2﹣2n]的值.
[(mn+n)2﹣2n]的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
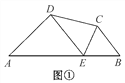
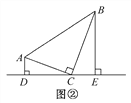
【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.
【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.
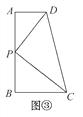
【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.
(1)请证明点P是四边形ABCD的边AB上的一个强相似点.
(2)若AD=3,BC=5,试求AB的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com