
【题目】如图,一张矩形纸片![]() .点
.点![]() 在这张矩形纸片的边
在这张矩形纸片的边![]() 上,将纸片折叠,使
上,将纸片折叠,使![]() 落在射线
落在射线![]() 上,折痕为
上,折痕为![]() ,点
,点![]() 分别落在点
分别落在点![]() 处,
处,
(1)若![]() ,则
,则![]() 的度数为 °;
的度数为 °;
(2)若![]() ,求
,求![]() 的长.
的长.

【答案】(1)![]() ;(2)3
;(2)3
【解析】
(1)根据折叠可得∠BFG=∠GFB′,再根据矩形的性质可得∠DFC=40°,从而∠BFG=70°即可得到结论;
(2) 首先求出GD=9-![]() =
=![]() ,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=
,由矩形的性质得出AD∥BC,BC=AD=9,由平行线的性质得出∠DGF=∠BFG,由翻折不变性可知,∠BFG=∠DFG,证出∠DFG=∠DGF,由等腰三角形的判定定理证出DF=DG=![]() ,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
,再由勾股定理求出CF,可得BF,再利用翻折不变性,可知FB′=FB,由此即可解决问题.
(1)根据折叠可得∠BFG=∠GFB′,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DGF=∠BFG,∠ADF=∠DFC,
∵![]()
∴∠DFC=40°
∴∠BFD=140°
∴∠BFG=70°
∴∠DGF=70°;
(2)∵AG=![]() ,AD=9,
,AD=9,
∴GD=9-![]() =
=![]() ,
,
∵四边形ABCD是矩形,
∴AD∥BC,BC=AD=9,
∴∠DGF=∠BFG,
由翻折不变性可知,∠BFG=∠DFG,
∴∠DFG=∠DGF,
∴DF=DG=![]() ,
,
∵CD=AB=4,∠C=90°,
∴在Rt△CDF中,由勾股定理得: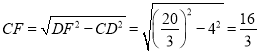 ,
,
∴BF=BC-CF=9-![]() ,
,
由翻折不变性可知,FB=FB′=![]() ,
,
∴B′D=DF-FB′=![]() -
-![]() =3.
=3.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图所示,四边形![]() 和
和![]() 分别是边长为
分别是边长为![]() 和
和![]() 的正方形.
的正方形.

(1)用含![]() 和
和![]() 的代数式表示图中三角形
的代数式表示图中三角形![]() 的面积.
的面积.
(2)用用![]() 和
和![]() 的代数式表示图中阴影部分的面积.
的代数式表示图中阴影部分的面积.
(3)小军计算出当![]() ,
,![]() 时的阴影部分面积,与小明计算的当
时的阴影部分面积,与小明计算的当![]() ,
,![]() 时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
时的阴影部分面积相等,为什么呢?请说明理由,并求出此时的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
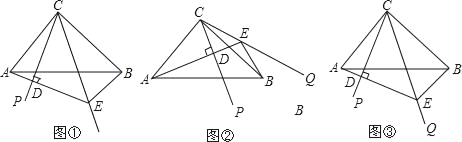
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入相应集合的括号内
+8.5, 0, -3.4, 12, -9, ![]() , 3.1415, -1.2,
, 3.1415, -1.2,![]() ,
, ![]()
(1)正数集合 { }
(2)整数集合 { }
(3)负分数集合 { }
(4)非正整数集合{ }
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,…,按此规律。则第(6)个图形中面积为1的正方形的个数为()

A. 20B. 25C. 35D. 27
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的是________(把所有正确结论的序号都选上).
(BC-AD),⑤四边形EFGH是菱形.其中正确的是________(把所有正确结论的序号都选上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com