
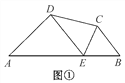
【题目】如图①,在四边形ABCD的边AB上任取一点E(点E不与A,B重合),分别连接ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.
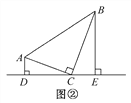
【试题再现】如图②,在△ABC中,∠ACB=90°,直角顶点C在直线DE上,分别过点A,B作AD⊥DE于点D,BE⊥DE于点E.求证:△ADC∽△CEB.
【问题探究】在图①中,若∠A=∠B=∠DEC=40°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由.
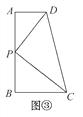
【深入探究】如图③,AD∥BC,DP平分∠ADC,CP平分∠BCD交DP于点P,过点P作AB⊥AD于点A,交BC于点B.
(1)请证明点P是四边形ABCD的边AB上的一个强相似点.
(2)若AD=3,BC=5,试求AB的长.
【答案】【试题再现】见解析;【问题探究】点E是四边形ABCD的边AB上的相似点. 理由见解析;【深入探究】(1) 点P是四边形ABCD的边AB上的一个强相似点,见解析;(2) ![]()
【解析】试题分析:【试题再现】易证∠BCE=∠CAD,又∠ADC=∠CEB=90°,故得△ADC∽△CEB.
【问题探究】要证明点E是四边形ABCD的AB边上的相似点,只要证明有一组三角形相似就行,很容易证明△ADE∽△BEC,所以问题得解.
【深入探究】(1)分别证明△ADP∽△PDC,△BPC∽△PDC,从而△ADP∽△PDC∽△BPC,故点P是四边形ABCD的边AB上的一个强相似点.
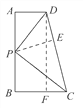
(2)过点P作PE⊥DC于点E,过点D作DF⊥BC于点F,则四边形ABFD是矩形,通过证明△ADP≌△EDP和△CBP≌△CEP得DC =8,再求出CF=2,在Rt△CDF中,由勾股定理,得AB=2![]() .
.
试题解析:【试题再现】
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
∵AD⊥DE,
∴∠ACD+∠CAD=90°,
∴∠BCE=∠CAD,
∵∠ADC=∠CEB=90°,
∴△ADC∽△CEB.
【问题探究】点E是四边形ABCD的边AB上的相似点.
理由如下:
∵∠DEC=40°,
∴∠DEA+∠CEB=140°.
∵∠A=40°,
∴∠ADE+∠AED=140°,
∴∠ADE=∠CEB,
又∵∠A=∠B,
∴△ADE∽△BEC,
∴点E是四边形ABCD的边AB上的相似点.
【深入探究】
(1)∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵DP平分∠ADC,CP平分∠BCD,
∴∠CDP+∠DCP=![]() (∠ADC+∠BCD)=90°,
(∠ADC+∠BCD)=90°,
∵DA⊥AB,DA∥BC,
∴CB⊥AB,
∴∠DPC=∠A=∠B=90°,
∵∠ADP=∠CDP,
∴△ADP∽△PDC,同理△BPC∽△PDC,
∴△ADP∽△PDC∽△BPC,即点P是四边形ABCD的边AB上的一个强相似点.
(2)过点P作PE⊥DC于点E,过点D作DF⊥BC于点F,则四边形ABFD是矩形,
∴DF=AB,
在△ADP与△EDP中,
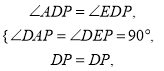
∴△ADP≌△EDP,
∴AD=DE,
同理△CBP≌△CEP,∴BC=EC,
∴DC=AD+BC=8.
在Rt△CDF中,CF=BC-BF=BC-AD=5-3=2,
由勾股定理,得DF=![]() =2
=2![]() ,
,
∴AB=2![]() .
.


科目:初中数学 来源: 题型:
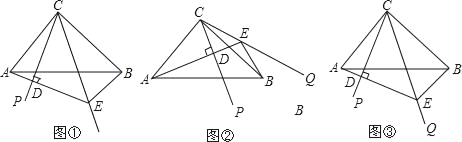
【题目】如图:在△ABC中,∠ACB=90°,AC=BC,∠PCQ=45°,把∠PCQ绕点C旋转,在整个旋转过程中,过点A作AD⊥CP,垂足为D,直线AD交CQ于E.
(1)如图①,当∠PCQ在∠ACB内部时,求证:AD+BE=DE;
(2)如图②,当CQ在∠ACB外部时,则线段AD、BE与DE的关系为_____;
(3)在(1)的条件下,若CD=6,S△BCE=2S△ACD,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22018的值,可令S=1+2+22+23+…+22018,则2S=2+22+23+24+…22019,因此2S﹣S=22019﹣1,即S=22019﹣1.依照以上的方法,计算出1+5+52+53+…52017的值为( )
A. 52018﹣1 B. 52019﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,小明同学在某月的日历上圈出![]() 个数,正方形的方框内的4个数的和是32,那么第1个数
个数,正方形的方框内的4个数的和是32,那么第1个数![]() 是.
是.
(2)如图2,玛丽也在上面的日历上圈出![]() 个数,斜框内的4个数的和是__________(用含
个数,斜框内的4个数的和是__________(用含![]() 的代数式表示);
的代数式表示);

(3)某月有5个星期日的和是75,则这个月中最后1个星期日是__________号;
(4)变式拓展:
若干个偶数按每行8个数排成如图:
①如图①,长方形方框内的9个数的和为__________.
②如图②,小丽所画的斜框内9个数,若它们的和为![]() ,则中间的数△为__________(用含
,则中间的数△为__________(用含![]() 的代数式表示).
的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
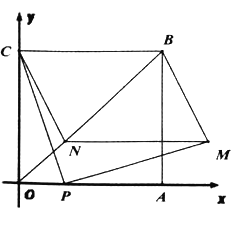
【题目】如图,在四边形![]() 是边长为4的正方形点P为OA边上任意一点(与点
是边长为4的正方形点P为OA边上任意一点(与点![]() 不重合),连接CP,过点P作
不重合),连接CP,过点P作![]() ,且
,且![]() ,过点M作
,过点M作![]() ,交
,交![]() 于点
于点![]() 联结
联结![]() ,设
,设![]() .
.
(1)当![]() 时,点
时,点![]() 的坐标为( , )
的坐标为( , )
(2)设![]() ,求出
,求出![]() 与
与![]() 的函数关系式,写出函数的定义域。
的函数关系式,写出函数的定义域。
(3)在![]() 轴正半轴上存在点
轴正半轴上存在点![]() ,使得
,使得![]() 是等腰三角形,请直接写出不少于4个符合条件的点
是等腰三角形,请直接写出不少于4个符合条件的点![]() 的坐标(用
的坐标(用![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E,F,G,H分别是BD,BC,AC,AD的中点,且AB=CD.下列结论:①EG⊥FH,②四边形EFGH是矩形,③HF平分∠EHG,④EG=![]() (BC-AD),⑤四边形EFGH是菱形.其中正确的是________(把所有正确结论的序号都选上).
(BC-AD),⑤四边形EFGH是菱形.其中正确的是________(把所有正确结论的序号都选上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一数轴上存在两动点,当第一次相遇后,速度都变为原来的两倍,第二次相遇后又都能恢复到原来的速度,则称这条数轴为魔幻数轴.
如图,已知一魔幻数轴上有A,O,B三点,其中A,O对应的数分别为﹣10,0,AB为47个单位长度,甲,乙分别从A,O两点同时出发,沿数轴正方向同向而行,甲的速度为3个单位/秒,乙的速度为1个单位/秒,甲到达点B后以当时速度立即返回,当甲回到点A时,甲、乙同时停止运动.
![]()
问:(1)点B对应的数为 ,甲出发 秒后追上乙(即第一次相遇)
(2)当甲到达点B立即返回后第二次与乙相遇,求出相遇点在数轴上表示的数是多少?
(3)甲、乙同时出发多少秒后,二者相距2个单位长度?(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )

A. m=-3n B. m=-![]() n C. m=-
n C. m=-![]() n D. m=
n D. m=![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com