
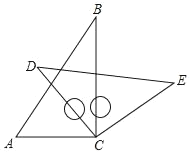
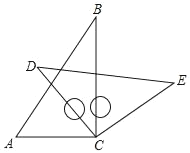
【题目】将一副三角板中的两块直角板中的两个直角顶点重合在一起,即按如图所示的方式叠放在一起,其中∠A=60°,∠B=30,∠D=45°.
(1)若∠BCD=45°,求∠ACE的度数.
(2)若∠ACE=150°,求∠BCD的度数.
(3)由(1)、(2)猜想∠ACE与∠BCD存在什么样的数量关系并说明理由.
【答案】(1)∠ACE=135°;(2)∠BCD=30°;(3)∠ACE与∠BCD互补.理由见解析.
【解析】
(1)先求得∠ACD的度数,即可得到∠ACE的度数;
(2)先求得∠ACD的度数,即可得到∠BCD的度数;
(3)依据∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,∠ACE=∠DCE+∠ACD=90°+∠ACD,即可得到∠ACE与∠BCD互补.
解:(1)∵∠BCD=45°,∠ACB=90°,
∴∠ACD=∠ACB﹣∠DCB=45°,
又∵∠DCE=90°,
∴∠ACE=∠ACD+∠DCE=45°+90°=135°;
(2)∵∠ACE=150°,∠DCE=90°,
∴∠ACD=∠ACE﹣∠DCE=150°﹣90°=60°,
又∵∠ACB=90°,
∴∠BCD=∠ACB﹣∠ACD=90°﹣60°=30°;
(3)由(1)、(2)猜想∠ACE与∠BCD互补.
理由:∵∠BCD=∠ACB﹣∠ACD=90°﹣∠ACD,
∠ACE=∠DCE+∠ACD=90°+∠ACD,
∴∠BCD+∠ACE=90°﹣∠ACD+90°+∠ACD=180°,
∴∠ACE与∠BCD互补.


科目:初中数学 来源: 题型:
【题目】如图,任意四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA上的点,对于四边形EFGH的形状,某班学生在一次数学活动课中,通过动手实践,探索出如下结论,其中错误的是( )
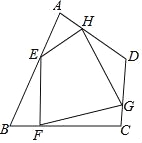
A.当E,F,G,H是各边中点,且AC=BD时,四边形EFGH为菱形
B.当E,F,G,H是各边中点,且AC⊥BD时,四边形EFGH为矩形
C.当E,F,G,H不是各边中点时,四边形EFGH可以为平行四边形
D.当E,F,G,H不是各边中点时,四边形EFGH不可能为菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足: (1)5(a+3)+2|b2|=0; (2)![]() x
x![]() y
y![]() +2a
+2a![]() b+c+1是七次多项式;
b+c+1是七次多项式;
求多项式ab[ab(2abcac3ab)4ac]abc的值..
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着移动互联网的快速发展,基于互联网的共享单车应运而生.为了解某小区居民使用共享单车的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数分别为:17,12,15,20,17,0,7,26,17,9.
(1)这组数据的中位数是 ,众数是 ;
(2)计算这10位居民一周内使用共享单车的平均次数;
(3)若该小区有200名居民,试估计该小区居民一周内使用共享单车的总次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合实践
问题情景:某综合实践小组进行废物再利用的环保小卫士行动. 他们准备用废弃的宣传单制作装垃圾的无盖纸盒.
操作探究:
⑴若准备制作一个无盖的正方体形纸盒,如图1,下面的哪个图形经过折叠能围成无盖正方体形纸盒?

⑵如图2是小明的设计图,把它折成无盖正方体形纸盒后与“保”字相对的是哪个字?
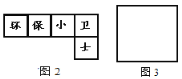
⑶如图3,有一张边长为20cm的正方形废弃宣传单,小华准备将其四角各剪去一个小正方形,折成无盖长方体形纸盒.
①请你在图3中画出示意图,用实线表示剪切线,虚线表示折痕.
②若四角各剪去了一个边长为xcm的小正方形,用含x的代数式表示这个纸盒的高为 cm,底面积为 cm2,当小正方形边长为4cm时,纸盒的容积为 cm3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一抛物线与x轴的交点是A(﹣2,0),B(1,0),且经过点C(2,8).
(1)求该抛物线的解析式.
(2)求该抛物线的顶点坐标.
(3)直接写出当y>8时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把下列各数填入表示它所在的数集的括号里
﹣(﹣2.3),![]() ,0,﹣
,0,﹣![]() ,30%,π,﹣|﹣2013|,﹣5
,30%,π,﹣|﹣2013|,﹣5![]() ,
,![]()
(1)负整数集合[ …]
(2)正有理数集合[ …]
(3)分数集合[ …]
查看答案和解析>>
科目:初中数学 来源: 题型:
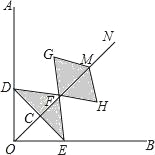
【题目】如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
A. y=![]() B. y=
B. y=![]() C. y=2
C. y=2![]() D. y=3
D. y=3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县第一届运动会需购买A,B两种奖品,若购买A种奖品4件和B种奖品3件,共需85元;若购买A种奖品3件和B种奖品1件,共需45元.
(1)求A、B两种奖品的单价各是多少元?
(2)运动会组委会计划购买A、B两种奖品共100件,购买费用不超过1150元,且A种奖品的数量不大于B种奖品数量的3倍,设购买A种奖品m件,购买总费用W元,写出W(元)与m(件)之间的函数关系式,求出自变量m的取值范围,并设计出购买总费用最少的方案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com