
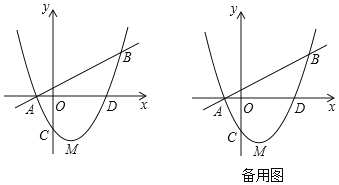
【题目】如图已知直线![]() 与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣
与抛物线y=ax2+bx+c相交于A(﹣1,0),B(4,m)两点,抛物线y=ax2+bx+c交y轴于点C(0,﹣![]() ),交x轴正半轴于D点,抛物线的顶点为M.
),交x轴正半轴于D点,抛物线的顶点为M.
(1)求抛物线的解析式;
(2)设点P为直线AB下方的抛物线上一动点,当△PAB的面积最大时,求△PAB的面积及点P的坐标;
(3)若点Q为x轴上一动点,点N在抛物线上且位于其对称轴右侧,当△QMN与△MAD相似时,求N点的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,P(
,P(![]() ,
,![]() );(3)N(3,0)或N(2+
);(3)N(3,0)或N(2+![]() ,1+
,1+![]() )或N(5,6)或N(
)或N(5,6)或N(![]() ,1﹣
,1﹣![]() ).
).
【解析】
(1)将点![]() 代入
代入![]() ,求出
,求出![]() ,将点
,将点![]() 代入
代入![]() ,即可求函数解析式; (2)如图,过
,即可求函数解析式; (2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,求出
,求出![]() 的解析式,设
的解析式,设![]() ,表示
,表示![]() 点坐标,表示
点坐标,表示![]() 长度,利用
长度,利用![]() ,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设
,建立二次函数模型,利用二次函数的性质求最值即可, (3)可证明△MAD是等腰直角三角形,由△QMN与△MAD相似,则△QMN是等腰直角三角形,设![]() ①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由
①当MQ⊥QN时,N(3,0); ②当QN⊥MN时,过点N作NR⊥x轴,过点M作MS⊥RN交于点S,由![]() (AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点
(AAS),建立方程求解; ③当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
R∥x轴,与过M点的垂线分别交于点S、R;可证△MQR≌△QNS(AAS),建立方程求解; ④当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,过点N作x轴的平行线,与两垂线交于点R、S;可证△MNR≌△NQS(AAS),建立方程求解.
解:(1)将点![]() 代入
代入![]() ,∴
,∴![]() ,
,
将点![]() 代入
代入![]() ,
,
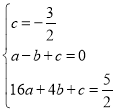 解得:
解得: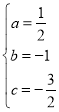 ,
,
∴函数解析式为![]() ;
;
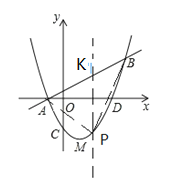
(2)如图,过![]() 作
作![]() 轴,交
轴,交![]() 于
于![]() ,设
,设![]() 为
为![]() ,
,
因为:![]() 所以:
所以:
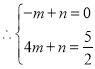 ,解得:
,解得: ,
,
所以直线AB为:![]() ,设
,设![]() ,则
,则![]() ,
,
所以:![]() ,
,
所以:![]()
![]() ,
,
当![]() ,
,![]() ,
,
此时:![]() .
.
(3)∵![]() ,
,
∴![]() ,
,
∴△MAD是等腰直角三角形.
∵△QMN与△MAD相似,∴△QMN是等腰直角三角形,
设![]()
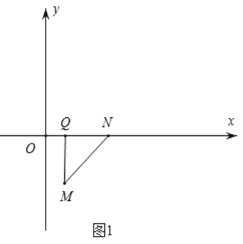
①如图1,当MQ⊥QN时,此时![]() 与
与![]() 重合,N(3,0);
重合,N(3,0);
②如图2,当QN⊥MN时,过点N作NR⊥x轴于![]() ,过点M作MS⊥RN交于点S.
,过点M作MS⊥RN交于点S.
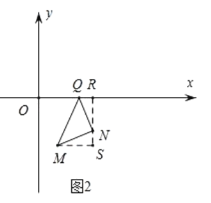
∵QN=MN,∠QNM=90°,∴![]() (AAS),
(AAS),![]()
∴![]() ,
,
∴![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
③如图3,当QN⊥MQ时,过点Q作x轴的垂线,过点N作NS∥x轴,过点![]() 作
作![]() R∥x轴,与过
R∥x轴,与过![]() 点的垂线分别交于点S、R;
点的垂线分别交于点S、R;
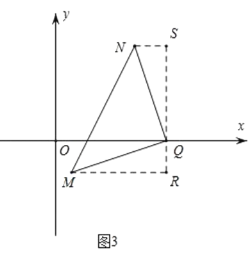
∵QN=MQ,∠MQN=90°,∴△MQR≌△QNS(AAS),![]() ,
,
![]() ,∴
,∴![]() ,∴t=5,(舍去负根)∴N(5,6);
,∴t=5,(舍去负根)∴N(5,6);
④如图4,当MN⊥NQ时,过点M作MR⊥x轴,过点Q作QS⊥x轴,
过点N作x轴的平行线,与两垂线交于点R、S;
∵QN=MN,∠MNQ=90°,∴△MNR≌△NQS(AAS),∴SQ=RN,
∴![]() ,∴
,∴![]() .
.
![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
综上所述:![]() 或
或![]() 或N(5,6)或
或N(5,6)或![]() .
.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
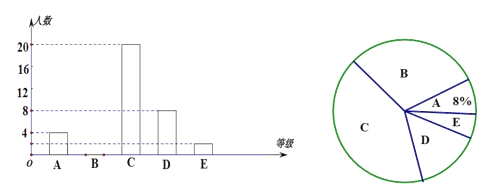
【题目】2020的寒假是一个特殊的假期.由于“新型冠状肺炎病毒”影响,学校的开学日期不断延后,在这期间某中学在学校微信公众号上积极鼓励学生静在家中沉下心来参加“静读名著”活动,活动以读名著的本书多少设为A,B,C,D,E五个等级,(本数依次为5,4,3,2,1),该校八(3)班全体学生参加了这次静在家中沉下心来读名著活动,芳芳同学通过调查并将这次读书阅读本数的结果绘制成如下两幅不完整的统计图.请根据图中信息,解答下列问题:
(1)该校八(3)班共有______学生;
(2)扇形统计图中B等级所对应扇形的圆心角等于______度;
(3)补全条形统计图;
(4)若该校有学生2500人读名著的本书在B、C级的人数一共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
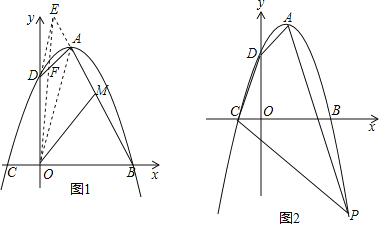
【题目】在平面直角坐标系xOy中,顶点为A的抛物线与x轴交于B、C两点,与y轴交于点D,已知A(1,4),B(3,0).
(1)求抛物线对应的二次函数表达式;
(2)探究:如图1,连接OA,作DE∥OA交BA的延长线于点E,连接OE交AD于点F,M是BE的中点,则OM是否将四边形OBAD分成面积相等的两部分?请说明理由;
(3)应用:如图2,P(m,n)是抛物线在第四象限的图象上的点,且m+n=﹣1,连接PA、PC,在线段PC上确定一点M,使AN平分四边形ADCP的面积,求点N的坐标.提示:若点A、B的坐标分别为(x1,y1)、(x2,y2),则线段AB的中点坐标为(![]() ,
,![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(新知探究)新定义:平面内两定点 A, B ,所有满足![]() k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
k ( k 为定值)的 P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”,
(问题解决)如图,在ABC 中,CB 4 , AB 2AC ,则ABC 面积的最大值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是_____.
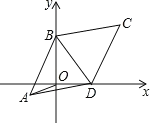
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解我市九年级学生身体素质情况,从全市九年级学生中随机抽取了部分学生进行了一次体育考试科目测试(把测试结果分为四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
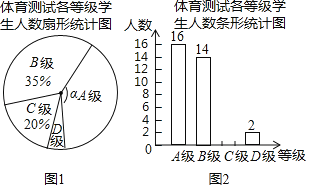
(1)本次抽样测试的学生人数是 ;
(2)图1中∠α的度数是 °,把图2条形统计图补充完整;
(3)全市九年级有学生6200名,如果全部参加这次体育科目测试,请估计不及格的人数为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一列数a1,a2,a3,…,a98,a99,a100,其中a3=2020,a7=-2018,a98=-1,且满足任意相邻三个数的和为常数,则a1+a2+a3+…+a98+a99+a100的值为( )
A.1985B.-1985C.2019D.-2019
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级同学最喜欢看哪一类课外书?某校随机抽取七年级部分同学对此进行问卷调査(每人只选择一种最喜欢的书籍类型).如图是根据调查结果绘制的两幅统计图(不完整).请根据统计图信息,解答下列问题:

(1)一共有多少名学生参与了本次问卷调查;
(2)补全条形统计图,并求出扇形统计图中“其他”所在扇形的圆心角度数;
(3)若该年级有400名学生,请你估计该年级喜欢“科普常识”的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用水平线和竖起线将平面分成若干个边长为1的小正方形格子,小正方形的顶点称为格点,以格点为顶点的多边形称为格点多边形.设格点多边形的面积为S,该多边形各边上的格点个数和为a,内部的格点个数为b,则![]() (史称“皮克公式”).
(史称“皮克公式”).
小明认真研究了“皮克公式”,并受此启发对正三角开形网格中的类似问题进行探究:正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,下图是该正三角形格点
中的两个多边形:
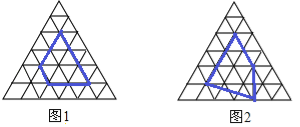
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点边多边形内部的格点个数 | 格点多边形的面积 | |
多边形1 | 8 | 1 | |
多边形2 | 7 | 3 | |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a、b之间的关系为S= (用含a、b的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com