
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌВЂЭъГЩЯргІШЮЮёЃК
ЛЦН№ЗжИю
ЬьЮФбЇМвПЊЦеРеАбЛЦН№ЗжИюГЦЮЊЩёЪЅЗжИюЃЌВЂжИГіБЯДяИчРЫЙЖЈРэЃЈЙДЙЩЖЈРэЃЉКЭЛЦН№ЗжИюЪЧМИКЮжаЕФЫЋБІЃЌЧАепКУБШЛЦН№ЃЌКѓепПАГЦжщБІЃЌРњЪЗЩЯзюдче§ЪНдкЪщжаЪЙгУЁАЛЦН№ЗжИюЁБетИіУћГЦЕФЪЧХЗФЗЃЌ19ЪРМЭвдКѓЁАЛЦН№ЗжИюЁБЕФЫЕЗЈж№НЅСїааЦ№РДЃЌЛЦН№ЗжИюБЛЙуЗКгІгУгкНЈжўЕШСьгђЃЎЛЦН№ЗжИюжИАбвЛЬѕЯпЖЮЗжЮЊСНВПЗжЃЌЪЙЦфжаНЯГЄВПЗжгыЯпЖЮзмГЄжЎБШЕШгкНЯЖЬВПЗжгыНЯГЄВПЗжжЎБШЃЌИУБШжЕЮЊ![]() ЃЎгУЯТУцЕФЗНЗЈЃЈШчЭМЂйЃЉОЭПЩвдзїГівбжЊЯпЖЮ
ЃЎгУЯТУцЕФЗНЗЈЃЈШчЭМЂйЃЉОЭПЩвдзїГівбжЊЯпЖЮ![]() ЕФЛЦН№ЗжИюЕу
ЕФЛЦН№ЗжИюЕу![]() ЃК
ЃК

ЂйвдЯпЖЮ![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЌ
ЃЌ
ЂкШЁ![]() ЕФжаЕу
ЕФжаЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ
ЂлбгГЄ![]() ЕН
ЕН![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЌ
ЃЌ
ЂмвдЯпЖЮ![]() ЮЊБпзїе§ЗНаЮ
ЮЊБпзїе§ЗНаЮ![]() ЃЌЕу
ЃЌЕу![]() ОЭЪЧЯпЖЮ
ОЭЪЧЯпЖЮ![]() ЕФЛЦН№ЗжИюЕуЃЎ
ЕФЛЦН№ЗжИюЕуЃЎ
вдЯТЪЧжЄУїЕу![]() ОЭЪЧЯпЖЮ
ОЭЪЧЯпЖЮ![]() ЕФЛЦН№ЗжИюЕуЕФВПЗжЙ§ГЬЃК
ЕФЛЦН№ЗжИюЕуЕФВПЗжЙ§ГЬЃК
жЄУїЃКЩше§ЗНаЮ![]() ЕФБпГЄЮЊ1ЃЌдђ
ЕФБпГЄЮЊ1ЃЌдђ![]() ЃЌ
ЃЌ
![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ
![]() ЃЌ
ЃЌ
![]() дк
дк![]() жаЃЌ
жаЃЌ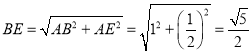 ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
Ё
ШЮЮёЃК
ЃЈ1ЃЉВЙШЋЬтжаЕФжЄУїЙ§ГЬЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЕу![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЕФЛЦН№ЗжИюЕуЃЌЗжБ№вд
ЕФЛЦН№ЗжИюЕуЃЌЗжБ№вд![]() ЮЊБпдкЯпЖЮ
ЮЊБпдкЯпЖЮ![]() ЭЌВрзїе§ЗНаЮ
ЭЌВрзїе§ЗНаЮ![]() КЭОиаЮ
КЭОиаЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЧѓжЄЃК
ЃЎЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЂлЃЌдке§ЮхБпаЮ![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() гы
гы![]() ЗжБ№НЛгкЕу
ЗжБ№НЛгкЕу![]() ЧѓжЄЃКЕу
ЧѓжЄЃКЕу![]() ЪЧ
ЪЧ![]() ЕФЛЦН№ЗжИюЕуЃЎ
ЕФЛЦН№ЗжИюЕуЃЎ
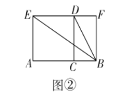
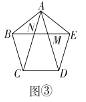
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉЯъМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉЩше§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌдђAB=AD=1ЃЌгЩЙДЙЩЖЈРэЕУГі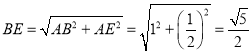 ЃЌЕУГі
ЃЌЕУГі![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌгЩе§ЗНаЮЕФаджЪЕУГі
ЃЌгЩе§ЗНаЮЕФаджЪЕУГі![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉгЩе§ЗНаЮКЭОиаЮЕФаджЪЕУГіЁЯEAB=ЁЯBCD=90ЁуЃЌAC=CD=AE=DE=BFЃЌBC=DFЃЌгЩЕуCЮЊЯпЖЮABЕФЛЦН№ЗжИюЕуЃЌЕУГі![]() ЃЌвђДЫ
ЃЌвђДЫ![]() ЃЌМДПЩЕУГіНсТлЃЛ
ЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉИљОне§ЮхБпаЮЕФаджЪЕУЕНЁЯDAE=ЁЯDAEЃЌЁЯADE=ЁЯAEM=36ЁуЃЌЭЦГіЁїAMEЁзЁїAEDЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУЕНЁрAEЃКAD=AMЃКAEЃЌЕУЕНAE2=ADAMЃЌЕШСПДњЛЛМДПЩЕУЕННсТлЃЎ
ЃЈ1ЃЉжЄУїЃКЩше§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌдђAB=AD=1ЃЌ
ЁпEЮЊADжаЕуЃЌ
ЁрAE=![]() ЃЌ
ЃЌ
ЁрдкRtЁїBAEжаЃЌ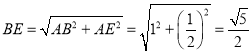
ЁпEF=BE
Ёр![]()
Ёр![]() ЃЌ
ЃЌ
ЁпЫФБпаЮAFGHЪЧе§ЗНаЮЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр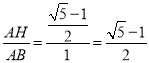 ЃЌ
ЃЌ
ЁрЕуHЪЧЯпЖЮABЕФЛЦН№ЗжИюЕуЃЛ
ЃЈ2ЃЉжЄУїЃКЁпЫФБпаЮACDEЪЧе§ЗНаЮЃЌЫФБпаЮCBFDЪЧОиаЮЃЌ
ЁрЁЯEAB=ЁЯBCD=90ЁуЃЌAC=CD=AE=DE=BFЃЌBC=DFЃЌ
ЁпЕуCЮЊЯпЖЮABЕФЛЦН№ЗжИюЕуЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЁїEABЁзЁїBCDЃЛ
ЃЈ3ЃЉжЄУїЃКЁпЮхБпаЮABCDEЪЧе§ЮхБпаЮЃЌ
ЁрЁЯBAE=ЁЯAED=![]() ЃЈ5-2ЃЉЁС180Ёу=108ЁуЃЌAB=AE=DEЃЌ
ЃЈ5-2ЃЉЁС180Ёу=108ЁуЃЌAB=AE=DEЃЌ
ЁрЁЯABE=ЁЯAEM=ЁЯDAE=ЁЯADE=![]() ЃЈ180Ёу-108ЁуЃЉ=36ЁуЃЌ
ЃЈ180Ёу-108ЁуЃЉ=36ЁуЃЌ
ЁпЁЯDAE=ЁЯDAEЃЌЁЯADE=ЁЯAEM=36ЁуЃЌ
ЁрЁїAMEЁзЁїAEDЃЌ
ЁрAEЃКAD=AMЃКAEЃЌ
ЁрAE2=ADAMЃЌ
ЁпAE=DE=DMЃЌ/span>
ЁрDM2=ADAMЃЌ
ЁрЕуMЪЧADЕФЛЦН№ЗжИюЕуЃЎ


 НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ
НЬбЇСЗаТЭЌВНСЗЯАЯЕСаД№АИ ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ
ПЮЧАПЮКѓЭЌВНСЗЯАЯЕСаД№АИ ПЮЬУаЁзївЕЯЕСаД№АИ
ПЮЬУаЁзївЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕ![]() жаЃЌе§ЗНаЮ
жаЃЌе§ЗНаЮ![]() ЕФБпГЄЮЊ2ЃЌКЏЪ§
ЕФБпГЄЮЊ2ЃЌКЏЪ§![]() ЕФЭМЯѓОЙ§ЕуBЃЌгыжБЯп
ЕФЭМЯѓОЙ§ЕуBЃЌгыжБЯп![]() НЛгкЕуDЃЎ
НЛгкЕуDЃЎ
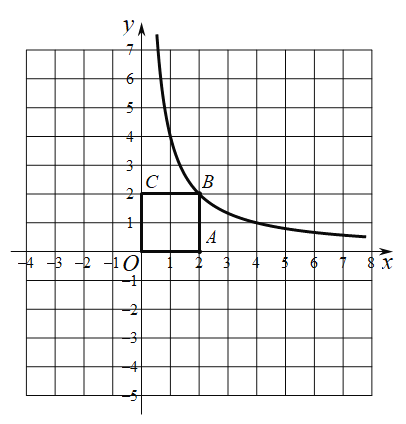
ЃЈ1ЃЉЧѓkЕФжЕЃЛ
ЃЈ2ЃЉжБЯп![]() гы
гы![]() БпЫљдкжБЯпНЛгкЕуMЃЌгыxжсНЛгкЕуNЃЎ
БпЫљдкжБЯпНЛгкЕуMЃЌгыxжсНЛгкЕуNЃЎ
ЂйЕБЕуDЮЊ![]() жаЕуЪБЃЌЧѓbЕФжЕЃЛ
жаЕуЪБЃЌЧѓbЕФжЕЃЛ
ЂкЕБ![]() ЪБЃЌНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіbЕФШЁжЕЗЖЮЇЃЎ
ЪБЃЌНсКЯКЏЪ§ЭМЯѓЃЌжБНгаДГіbЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ![]() ЕФе§ЗНаЮABCDжаЃЌЕуEЃЌFЪЧЖдНЧЯпACЕФШ§ЕШЗжЕуЃЌЕуPдке§ЗНаЮЕФБпЩЯЃЌдђТњзуPE+PF=
ЕФе§ЗНаЮABCDжаЃЌЕуEЃЌFЪЧЖдНЧЯпACЕФШ§ЕШЗжЕуЃЌЕуPдке§ЗНаЮЕФБпЩЯЃЌдђТњзуPE+PF=![]() ЕФЕуPЕФИіЪ§ЪЧЃЈ ЃЉ
ЕФЕуPЕФИіЪ§ЪЧЃЈ ЃЉ

A.0B.4C.8D.16
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
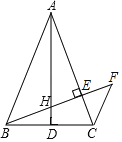
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌABЃНACЃЌADЪЧБпBCЩЯЕФжаЯпЃЌBEЁЭACгкЕуEЃЌНЛADгкЕуHЙ§ЕуCзїCFЁЮABНЛBEЕФбгГЄЯпгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABHЁзЁїBFCЃЛ
ЃЈ2ЃЉЧѓжЄЃКBH2ЃНHEHFЃЛ
ЃЈ3ЃЉШєABЃН2ЃЌЁЯBACЃН45ЁуЃЌЧѓBHЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЪЧ
ЪЧ![]() ЕФЦНЗжЯпЃЌОЙ§
ЕФЦНЗжЯпЃЌОЙ§![]() СНЕуЕФдВЕФдВаФ
СНЕуЕФдВЕФдВаФ![]() ЧЁКУТфдк
ЧЁКУТфдк![]() ЩЯЃЌ
ЩЯЃЌ![]() ЗжБ№гы
ЗжБ№гы![]() НЛгкЕу
НЛгкЕу![]() ЃЎШє
ЃЎШє![]() ЃЎдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
ЃЎдђЭМжавѕгАВПЗжЕФУцЛ§ЮЊЃЈ ЃЉ
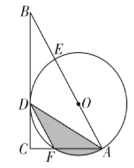
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОйааСЫздЙБЪаДДНЈШЋЙњЮФУїГЧЪажЊЪЖОКШќЛюЖЏЃЌГѕвЛФъМЖШЋЬхЭЌбЇВЮМгСЫжЊЪЖОКШќЃЎ
ЪеМЏНЬОнЃКЯжЫцЛњГщШЁСЫГѕвЛФъМЖ![]() УћЭЌбЇЕФЁАДДЮФжЊЪЖОКШќЁБГЩМЈЃЌЗжЪ§ШчЯТЃЈЕЅЮЛЃКЗжЃЉЃК
УћЭЌбЇЕФЁАДДЮФжЊЪЖОКШќЁБГЩМЈЃЌЗжЪ§ШчЯТЃЈЕЅЮЛЃКЗжЃЉЃК
ећРэЗжЮіЪ§ОнЃК
ГЩМЈ | ЦЕЪ§ЃЈШЫЪ§ЃЉ |
|
|
|
|
|
|
|
|
ЃЈ1ЃЉЧыНЋЭМБэжаПеШБЕФВПЗжВЙГфЭъећЃЛ
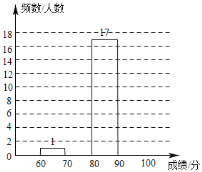
ЃЈ2ЃЉбЇаЃОіЖЈБэеУЁАДДЮФжЊЪЖОКШќЁБГЩМЈдк![]() ЗжМАЦфвдЩЯЕФЭЌбЇЃЎИљОнЩЯУцЭГМЦНсЙћЙРМЦИУаЃГѕвЛФъМЖ
ЗжМАЦфвдЩЯЕФЭЌбЇЃЎИљОнЩЯУцЭГМЦНсЙћЙРМЦИУаЃГѕвЛФъМЖ![]() ШЫжаЃЌдМгаЖрЩйШЫНЋЛёЕУБэеУЃЛ
ШЫжаЃЌдМгаЖрЩйШЫНЋЛёЕУБэеУЃЛ
ЃЈ3ЃЉЁАДДЮФжЊЪЖОКШќЁБжаЃЌЪмЕНБэеУЕФаЁКьЭЌбЇЕУЕНСЫгЁгаЙЈЩШЁЂМєжНЁЂВЪЕЦЁЂПжСњЭМАИЕФЫФУЖМЭФюеТЃЌЫ§ДгжабЁШЁСНУЖЫЭИјЕмЕмЃЌдђаЁКьЫЭИјЕмЕмЕФСНУЖМЭФюеТжаЃЌЧЁКУгаПжСњЭМАИЕФИХТЪЪЧ______________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
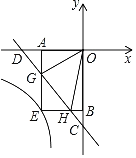
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌжБЯпyЃНЉxЉ2гыxжсЃЌyжсЗжБ№НЛгкЕуDЃЌCЃЎЕуGЃЌHЪЧЯпЖЮCDЩЯЕФСНИіЖЏЕуЃЌЧвЁЯGOHЃН45ЁуЃЌЙ§ЕуGзїGAЁЭxжсгкAЃЌЙ§ЕуHзїHBЁЭyжсгкBЃЌбгГЄAGЃЌBHНЛгкЕуEЃЌдђЙ§ЕуEЕФЗДБШР§КЏЪ§yЃН![]() ЕФНтЮіЪНЮЊ_____ЃЎ
ЕФНтЮіЪНЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
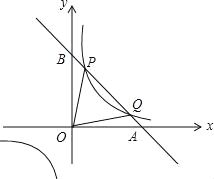
ЁОЬтФПЁПвбжЊжБЯпy=kx+bгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§НЛгквЛЯѓЯоФкЕФPЃЈ![]() ЃЌnЃЉЃЌQЃЈ4ЃЌmЃЉСНЕуЃЌЧвtanЁЯBOP=
ЃЌnЃЉЃЌQЃЈ4ЃЌmЃЉСНЕуЃЌЧвtanЁЯBOP=![]() ЃК
ЃК
ЃЈ1ЃЉЧѓЗДБШР§КЏЪ§КЭжБЯпЕФКЏЪ§БэДяЪНЃЛ
ЃЈ2ЃЉЧѓЁїOPQЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
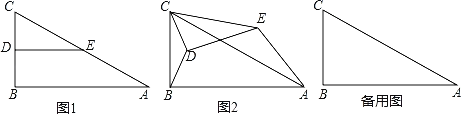
ЁОЬтФПЁПШчЭМ1ЃЌдкRtЁїABCжаЃЌЁЯBЃН90ЁуЃЌABЃН4ЃЌBCЃН2ЃЌЕуDЁЂEЗжБ№ЪЧБпBCЁЂACЕФжаЕуЃЌСЌНгDEЃЎНЋЁїCDEШЦЕуCФцЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊІСЃЎ
ЃЈ1ЃЉЮЪЬтЗЂЯж
ЂйЕБІСЃН0ЁуЪБЃЌ![]() ЃН_______ЃЛ
ЃН_______ЃЛ
ЂкЕБІСЃН180ЁуЪБЃЌ![]() ЃН______ЃЎ
ЃН______ЃЎ
ЃЈ2ЃЉЭиеЙЬНОП
ЪдХаЖЯЃКЕБ0ЁуЁмІСЃМ360ЁуЪБЃЌ![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЃЈ3ЃЉЮЪЬтНтОі
ЁїCDEШЦЕуCФцЪБеыа§зЊжСAЁЂBЁЂEШ§ЕудкЭЌвЛЬѕжБЯпЩЯЪБЃЌЧѓЯпЖЮBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com