
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为2,函数
的边长为2,函数![]() 的图象经过点B,与直线
的图象经过点B,与直线![]() 交于点D.
交于点D.
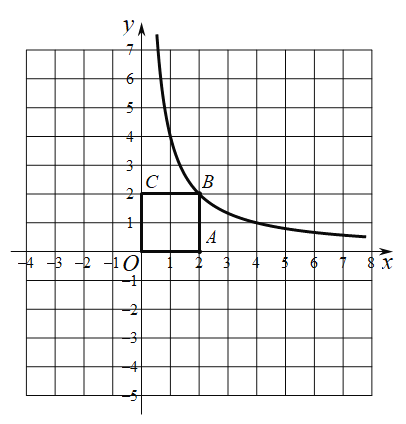
(1)求k的值;
(2)直线![]() 与
与![]() 边所在直线交于点M,与x轴交于点N.
边所在直线交于点M,与x轴交于点N.
①当点D为![]() 中点时,求b的值;
中点时,求b的值;
②当![]() 时,结合函数图象,直接写出b的取值范围.
时,结合函数图象,直接写出b的取值范围.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]()
【解析】
(1)把![]() 代入
代入![]() ,求解即可;
,求解即可;
(2)①根据题意得出D的坐标为(4,1),代入![]() 即可;
即可;
②当D在BC上方时,得D的坐标为(1,4),代入![]() ,得
,得![]() ,即可得到b的取值范围.
,即可得到b的取值范围.
(1)把![]() 代入
代入![]() ,
,
解得:![]() ;
;
(2)①如图:
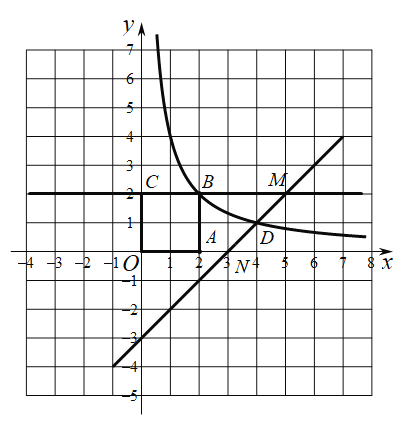
当点D为![]() 中点时,可得D的纵坐标为1,
中点时,可得D的纵坐标为1,
代入![]() 得x=4,
得x=4,
∴![]()
代入![]() 得:
得:![]() ;
;
②当D在BC上方双曲线上时,
当D点到直线BC的距离大于2时,
DM>MN,
当D点到直线BC的距离等于2时,D点纵坐标为4
∴D点纵坐标为4,代入![]() 得横坐标为1,
得横坐标为1,
∴D的坐标为(1,4),
把D(1,4)代入![]() ,
,
得:![]() ,
,
∴当![]() 时,DM=MN,
时,DM=MN,
当![]() 时,DM>MN,
时,DM>MN,
当D在BC下方双曲线上时,
DM<MN,不符合题意,
故b的取值范围是![]() .
.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
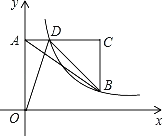
【题目】如图,在平面直角坐标系中,点A在y轴正半轴上,AC∥x轴,点B、C的横坐标都是3,且BC=2,点D在AC上,若反比例函数y=![]() (x>0)的图象经过点B、D.且AO:BC=3:2.
(x>0)的图象经过点B、D.且AO:BC=3:2.
(1)求点D坐标;
(2)将△AOD沿着OD折叠,设顶点A的对称点为A′,试判断点A′是否恰好落在直线BD上,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为M(2,-4),且过点A(-1,5),连接AM交x轴于点B.
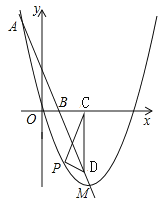
(1)求这条抛物线的解析式;
(2)求点B的坐标;
(3)设点P(x,y)是抛物线在x轴下方、顶点左方一段上的动点,连接PO,过以P为顶角顶点、PO为腰的等腰三角形的另一顶点C作x轴的垂线交直线AM于点D,连结PD,设△PCD的面积为S,求S与x之间的函数关系式;
(4)在上述动点P(x,y)中,是否存在使![]() =2的点?若存在,求点P的坐标;若不存在,说明理由.
=2的点?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,以BC为直径作半圆O,以点D为圆心、DA为半径做圆弧交半圆O于点P.连结DP并延长交AB于点E.
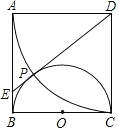
(1)求证:DE为半圆O的切线;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 的直线交
的直线交![]() 于
于![]() ,交射线
,交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
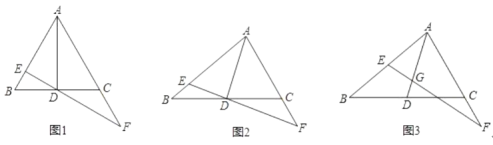
(1)如图1,若![]() 为等边三角形,点
为等边三角形,点![]() 与
与![]() 重合,
重合,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 与
与![]() 重合,求证:
重合,求证:![]() ;
;
(3)如图3,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】疫情期间某校学生积极观看网络直播课程,为了了解全校500名学生观看网络直播课程的情况,随机抽取50名学生,对他们观看网络直播课程的节数进行收集,并对数据进行了整理、描述和分析,下面给出了部分信息.
观看直播课节数的频数分布表
节数x | 频数 | 频率 |
| 8 | 0.16 |
| 10 | 0.20 |
| 16 |
|
|
| 0.24 |
| 4 | 0.08 |
总数 | 50 | 1 |

其中,节数在![]() 这一组的数据是:
这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() __________,
__________,![]() __________
__________
(2)请补全频数分布直方图;
(3)随机抽取的50名学生观看直播课节数的中位数是___________;
(4)请估计该校学生中观看网络直播课节数不低于30次的约有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
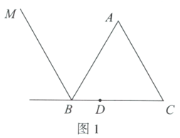
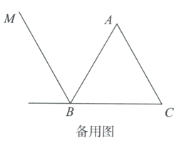
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肆虐全球,某地区有一外来无症状感染者,没有有效隔离,经过两轮传染后共有121人患了流感.
(1)每轮传染中平均一个人传染了多少个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,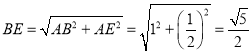 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
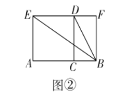
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
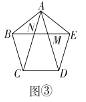
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com