练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】2020年新型冠状病毒肆虐全球，某地区有一外来无症状感染者，没有有效隔离，经过两轮传染后共有121人患了流感．

    （1）每轮传染中平均一个人传染了多少个人？

    （2）如果不及时控制，第三轮将又有多少人被传染？

    【答案】（1）每轮传染中平均一个人传染了10个人；（2）如果不及时控制，第三轮将又有1331人被传染．

    【解析】

    （1）根据题意可设平均一个人传染了x个人，可列出方程1+x+（1+x）x=121，即可得出结果.（2）用第二轮被传染的人数乘以平均每人传染的人数即可得出结果.

    （1）设每轮传染中平均一个人传染了x个人．

    1+x+（1+x）x=121.

    解得x=10或x=-12（舍去）

    答：每轮传染中平均一个人传染了10个人.

    （2）12111=1331（人）.

    答：如果不及时控制，第三轮将又有1331人被传染．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温，体温正常方可进校．

    （1）甲同学在A入口处测量体温的概率是 ；

    （2）求甲、乙两位同学在同一入口处测量体温的概率．（用“画树状图”或“列表”的方法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，正方形的边长为2，函数的图象经过点B，与直线交于点D．

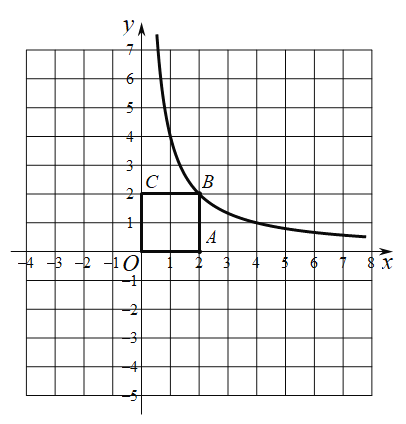
    （1）求k的值；

    （2）直线与边所在直线交于点M，与x轴交于点N．

    ①当点D为中点时，求b的值；

    ②当时，结合函数图象，直接写出b的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在正方形中，，、是对角线上的两个动点(点靠近点)，且，是正方形四边上的任意一点．若是等边三角形，则 AE的长为______ ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】二次函数的图象经过点（0，-4）和（-2，2）.

    （1）求的值，并用含的式子表示；

    （2）求证：此抛物线与轴有两个不同交点；

    （3）当时，若二次函数满足随的增大而减小，求的取值范围；

    (4) 直线上有一点（，5），将点向右平移4个单位长度，得到点，若抛物线与线段只有一个公共点，求的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市各学校积极响应上级“停课不停教、修课不停学”的要求，开展了空中在线教学.其校就“网络直播课”的满意度进行了随机在线问卷调在，调在结果分为四类: A.非常满意；B.很满意；C.一般；D.不满意，将收集到的信息进行了统计，绘制成如下不完整的统计表和统计图(如图所示).请你根据统计图表所提供的信息解答下列问题:

    （1）接受问卷调查的学生共有__ _人； ； ；

    （2）补全条形统计图；

    频数分布统计表

    类别

    频数

    频率

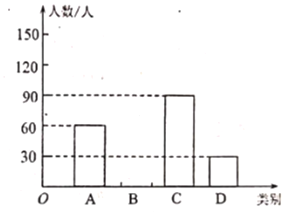
    （3）若该校共有学生人，请你根据上述调查结果，估计该校对“网络直播课”满意度为类和类的学生共有多少人；

    （4）为改进教学，学校决定从选填结果是类的学生中，选取甲、乙、丙、丁四人，随机抽取两名同学参与网络座谈会，求甲、乙两名同学同时被抽中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在边长为的正方形ABCD中，点E，F是对角线AC的三等分点，点P在正方形的边上，则满足PE+PF=的点P的个数是（ ）

    A.0B.4C.8D.16

    查看答案和解析>>

    科目：初中数学 来源： 题型：

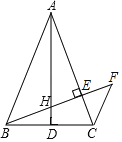
    【题目】如图，在△ABC中，AB＝AC，AD是边BC上的中线，BE⊥AC于点E，交AD于点H过点C作CF∥AB交BE的延长线于点F．

    （1）求证：△ABH∽△BFC；

    （2）求证：BH2＝HEHF；

    （3）若AB＝2，∠BAC＝45°，求BH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

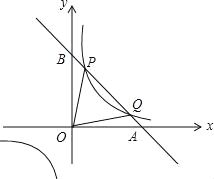
    【题目】已知直线y=kx+b与x轴、y轴分别交于A、B两点，与反比例函数交于一象限内的P（，n），Q（4，m）两点，且tan∠BOP=：

    （1）求反比例函数和直线的函数表达式；

    （2）求△OPQ的面积．

    查看答案和解析>>

    同步练习册答案