
【题目】二次函数![]() 的图象经过点
的图象经过点![]() (0,-4)和
(0,-4)和![]() (-2,2).
(-2,2).
(1)求![]() 的值,并用含
的值,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:此抛物线与![]() 轴有两个不同交点;
轴有两个不同交点;
(3)当![]() 时,若二次函数满足
时,若二次函数满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围;
的取值范围;
(4) 直线![]() 上有一点
上有一点![]() (
(![]() ,5),将点
,5),将点![]() 向右平移4个单位长度,得到点
向右平移4个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,b=2a-3;(2)见解析;(3)
,b=2a-3;(2)见解析;(3)![]() ≤a<0或0< a≤
≤a<0或0< a≤![]() ;(4)0<a<4或
;(4)0<a<4或![]() .
.
【解析】
(1)把A(0,-4)和B(-2,2)代入到二次函数关系式中即可得出答案;
(2)判断![]() 的符号即可;
的符号即可;
(3)当![]() 时,抛物线的对称轴需满足
时,抛物线的对称轴需满足![]() ≥0;当
≥0;当![]() 时,对称轴需满足
时,对称轴需满足![]() ≤-2,分这两种情况求解即可;
≤-2,分这两种情况求解即可;
(4)当a>0时,满足点(1,a+2a-3-4)在D点的下方,即a+2a-3-4<5即可;当a<0时,抛物线与线段只有一个公共点,即顶点的纵坐标为5,即可得出答案.
(1)解:把点A(0,-4)和B(-2,2)分别代入y=ax2+bx+c中,得c=-4,4a-2b+c=2.
∴b=2a-3.
(2)证明:

对于任意的![]() ,都有
,都有![]() ,
,
∴此抛物线与![]() 轴有两个不同交点;
轴有两个不同交点;
(3)解:当a<0时,依题意抛物线的对称轴需满足![]() ≤-2,
≤-2,
解得![]() ≤a<0,
≤a<0,
当a>0时,依题意抛物线的对称轴需满足![]() ≥0,
≥0,
解得 0< a≤![]() ,
,
∴a的取值范围是![]() ≤a<0或0< a≤
≤a<0或0< a≤![]() .
.
(4)解:设AB表达式为![]() ,
,
把点A(0,-4)和B(-2,2)代入得到:
![]() ,解得:
,解得:![]() ,
,
∴直线AB的表达式为y=-3x-4,把C(m,5)代入得m=-3,
∴C(-3,5),由平移得D(1,5),
①当a>0时,若抛物线与线段CD只有一个公共点,
(如图1),则抛物线上的点(1,a+2a-3-4)在D点的下方,
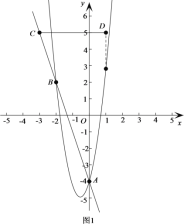
∴a+2a-3-4<5,
解得a<4,
∴0<a<4;
②当a<0时,若抛物线的顶点在线段CD上,则抛物线与线段只有一个公共点.(如图2)
∴![]() .即
.即![]() ,
,
解得![]() (舍去)或
(舍去)或![]() ,
,
综上,a的取值范围是0<a<4或![]() .
.



 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】(2016宁夏)某种水彩笔,在购买时,若同时额外购买笔芯,每个优惠价为3元,使用期间,若备用笔芯不足时需另外购买,每个5元.现要对在购买水彩笔时应同时购买几个笔芯作出选择,为此收集了这种水彩笔在使用期内需要更换笔芯个数的30组数据,整理绘制出下面的条形统计图:
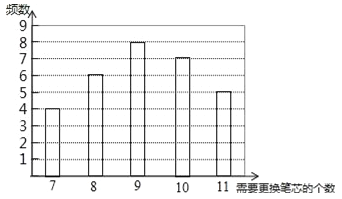
设x表示水彩笔在使用期内需要更换的笔芯个数,y表示每支水彩笔在购买笔芯上所需要的费用(单位:元),n表示购买水彩笔的同时购买的笔芯个数.
(1)若n=9,求y与x的函数关系式;
(2)若要使这30支水彩笔“更换笔芯的个数不大于同时购买笔芯的个数”的频率不小于0.5,确定n的最小值;
(3)假设这30支笔在购买时,每支笔同时购买9个笔芯,或每支笔同时购买10个笔芯,分别计算这30支笔在购买笔芯所需费用的平均数,以费用最省作为选择依据,判断购买一支水彩笔的同时应购买9个还是10个笔芯.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 中,
中,![]() 是
是![]() 的中点,点
的中点,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() 重合),过点
重合),过点![]() 的直线交
的直线交![]() 于
于![]() ,交射线
,交射线![]() 于点
于点![]() ,设
,设![]() ,
,![]() .
.
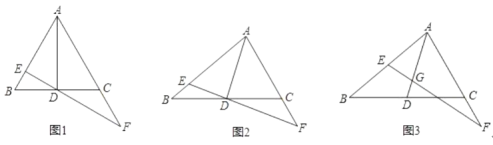
(1)如图1,若![]() 为等边三角形,点
为等边三角形,点![]() 与
与![]() 重合,
重合,![]() ,求证:
,求证:![]() ;
;
(2)如图2,若点![]() 与
与![]() 重合,求证:
重合,求证:![]() ;
;
(3)如图3,若![]() ,
,![]() ,
,![]() ,直接写出
,直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
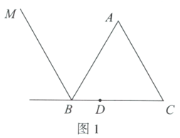
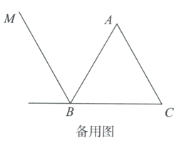
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新冠肺炎疫情发生以来,我市广大在职党员积极参与社区防疫工作,助力社区坚决打赢疫情防控阻击战.其中,A社区有500名在职党员,为了解本社区2月—3月期间在职党员参加应急执勤的情况,A社区针对执勤的次数随机抽取50名在职党员进行调查,并对数据进行了整理、描述和分析,下面给出了部分信息.
次数x/次 | 频数 | 频率 |
0 ≤x< 10 | 8 | 0.16 |
10≤x< 20 | 10 | 0.20 |
20≤x< 30 | 16 | b |
30≤x< 40 | a | 0.24 |
x≥ 40 | 4 | 0.08 |

其中,应急执勤次数在20≤x< 30这一组的数据是:
20 20 21 22 23 23 23 23 25 26 26 26 27 28 28 29
请根据所给信息,解答下列问题:
(1)![]() = ,
= ,![]() = ;
= ;
(2)请补全频数分布直方图;
(3)随机抽取的50名在职党员参加应急执勤次数的中位数是 ;
(4)请估计2月—3月期间A社区在职党员参加应急执勤的次数不低于30次的约有__人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肆虐全球,某地区有一外来无症状感染者,没有有效隔离,经过两轮传染后共有121人患了流感.
(1)每轮传染中平均一个人传染了多少个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ;
;
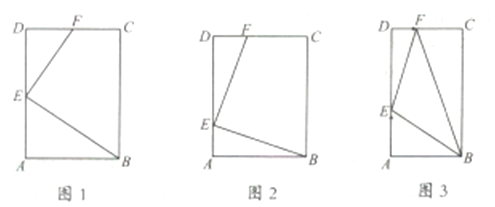
①如图![]() ,若
,若![]() ,且点
,且点![]() 是
是![]() 中点,求证
中点,求证![]() ;
;
②如图![]() ,若
,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,当
,当![]() ,
,![]() 时,点
时,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,当点
,当点![]() 到
到![]() 时两点都停止运动,则点
时两点都停止运动,则点![]() 的运动时间
的运动时间![]() 为多少时,
为多少时,![]() 的面积
的面积![]() 最小,最小面积为多少?
最小,最小面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com