
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
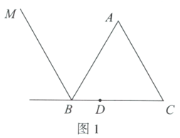
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
【答案】(1)图见解析;(2)证明见解析;(3)①证明见解析; ②20°.
【解析】
(1)根据题意,射线![]() 顺时针旋转60°,用尺规作图法,做出∠DAE = ∠C = 60°,再连接DE,即完成作图;
顺时针旋转60°,用尺规作图法,做出∠DAE = ∠C = 60°,再连接DE,即完成作图;
(2)在等边三角形ABC中,由![]() 可得出
可得出![]() ;由射线
;由射线![]() 绕点A顺时针旋转60°得到射线
绕点A顺时针旋转60°得到射线![]() ,可得∠DAE =
,可得∠DAE =![]() ,进而得出
,进而得出![]() ;由
;由![]() 平分∠ABC的外角
平分∠ABC的外角![]() 可得
可得![]() ,进而推出
,进而推出![]() ,由此可证
,由此可证![]() (ASA),再根据三角形全等的性质易证
(ASA),再根据三角形全等的性质易证![]() ;
;
(3)①连接![]() ,设
,设![]() ,根据点B与点F关于直线
,根据点B与点F关于直线![]() 对称的性质可得
对称的性质可得![]() ,
,![]() ;由
;由![]() 易得
易得![]() ;在等边三角形
;在等边三角形![]() 中, 由
中, 由![]() ,
,![]() ,易证
,易证![]() ,
,![]() ,又因为
,又因为![]() ,再根据三角形AFC的内角和定理,可推出
,再根据三角形AFC的内角和定理,可推出![]() ,和前面的证明联立可得
,和前面的证明联立可得![]() ,所以同旁内角互补,
,所以同旁内角互补,![]() .
.
②通过图中各个三角形的内角和之间的关系,设∠BAD=α,通过证明∠CFA=∠COF推论出![]() ,即可计算出∠BAD=20°.
,即可计算出∠BAD=20°.
(1)依题意补全图形
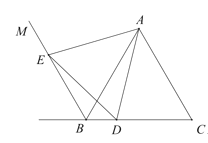
(2)证明:
∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
∴![]() .
.
∵射线![]() 绕点A顺时针旋转60°得到射线
绕点A顺时针旋转60°得到射线![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.

(3)①证明:连接![]() ,设
,设![]() ,
,
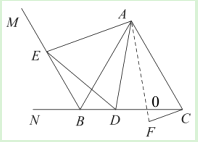
∵点B与点F关于直线![]() 对称,
对称,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() .
.
∵等边三角形![]() 中,
中,![]() ,
,
∴![]()
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
且![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
② 由① 知 ![]() ,
,![]()
∴∠EAF=∠F=![]()
∴∠DAF = α,
∵![]() ,由②知BE=CD
,由②知BE=CD
∴BD=CF
∴∠CFA=∠COF
∴![]()
∴3α=60°
∴α=20°


科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
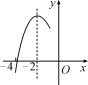
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
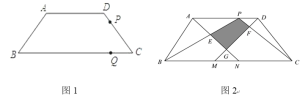
(1)梯形ABCD的面积等于 .
(2)如图1,动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.当PQ∥AB时,P点离开D点多少时间?
(3)如图2,点K是线段AD上的点,M、N为边BC上的点,BM=CN=5,连接AN、DM,分别交BK、CK于点E、F,记△ ADG和△ BKC重叠部分的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为2,函数
的边长为2,函数![]() 的图象经过点B,与直线
的图象经过点B,与直线![]() 交于点D.
交于点D.
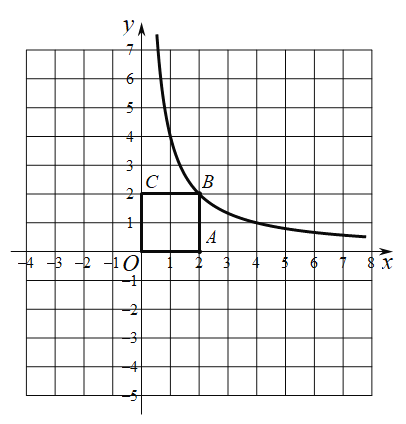
(1)求k的值;
(2)直线![]() 与
与![]() 边所在直线交于点M,与x轴交于点N.
边所在直线交于点M,与x轴交于点N.
①当点D为![]() 中点时,求b的值;
中点时,求b的值;
②当![]() 时,结合函数图象,直接写出b的取值范围.
时,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小王同学“过直线外一点作该直线的平行线”的尺规作图过程.
已知:直线l及直线l外一点P.
求作:直线![]() ,使得
,使得![]() .
.

作法:如图,
①在直线l外取一点A,作射线![]() 与直线l交于点B,
与直线l交于点B,
②以A为圆心,![]() 为半径画弧与直线l交于点C,连接
为半径画弧与直线l交于点C,连接![]() ,
,
③以A为圆心,![]() 为半径画弧与线段
为半径画弧与线段![]() 交于点
交于点![]() ,
,
则直线![]() 即为所求.
即为所求.
根据小王设计的尺规作图过程,,
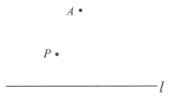
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵![]() ,
,
∴![]() ,(______________________)(填推理的依据).
,(______________________)(填推理的依据).
∵![]() __________,
__________,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() (____________________)(填推理的依据).
(____________________)(填推理的依据).
即![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图象经过点
的图象经过点![]() (0,-4)和
(0,-4)和![]() (-2,2).
(-2,2).
(1)求![]() 的值,并用含
的值,并用含![]() 的式子表示
的式子表示![]() ;
;
(2)求证:此抛物线与![]() 轴有两个不同交点;
轴有两个不同交点;
(3)当![]() 时,若二次函数满足
时,若二次函数满足![]() 随
随![]() 的增大而减小,求
的增大而减小,求![]() 的取值范围;
的取值范围;
(4) 直线![]() 上有一点
上有一点![]() (
(![]() ,5),将点
,5),将点![]() 向右平移4个单位长度,得到点
向右平移4个单位长度,得到点![]() ,若抛物线与线段
,若抛物线与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为![]() 的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=
的正方形ABCD中,点E,F是对角线AC的三等分点,点P在正方形的边上,则满足PE+PF=![]() 的点P的个数是( )
的点P的个数是( )

A.0B.4C.8D.16
查看答案和解析>>
科目:初中数学 来源: 题型:
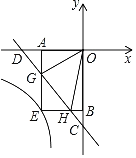
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com