
【题目】如图,在平面直角坐标系xOy中,直线y=﹣x﹣2与x轴,y轴分别交于点D,C.点G,H是线段CD上的两个动点,且∠GOH=45°,过点G作GA⊥x轴于A,过点H作HB⊥y轴于B,延长AG,BH交于点E,则过点E的反比例函数y=![]() 的解析式为_____.
的解析式为_____.
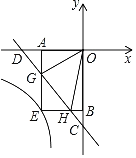
【答案】y=![]()
【解析】
过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,设点A(-![]() ,0)则AO=
,0)则AO=![]() ,DO=2,AD=2-
,DO=2,AD=2-![]() ,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-
,由“AAS”可证△GAO≌△PNG,可得NP=AG=2-![]() ,AO=GN=
,AO=GN=![]() ,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
,可求点P坐标,求出一次函数解析式,可求点H的纵坐标,即可求解.
解:如图,过点G作GP⊥GO,交OH的延长线于点P,过点P作PN⊥AE,交AE延长线于N,
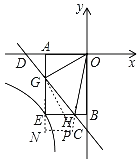
设点A(-![]() ,0)
,0)
∴AO=![]() ,
,
∵直线y=﹣x﹣2与x轴,y轴分别交于点D,C,
∴点D(﹣2,0),∠ADC=45°,
∴DO=2,AD=2﹣![]() ,
,
∵AE⊥OD,
∴∠ADG=∠AGD=45°,
∴AD=AG=2﹣![]() ,
,
∵GP⊥GO,∠GOH=45°,
∴∠GPO=∠GOP=45°,
∴GP=GO,
∵∠AGO+∠AOG=90°,∠AGO+∠NGP=90°,
∴∠AOG=∠NGP,
又∵∠GNP=∠GAO=90°,GO=GP,
∴△GAO≌△PNG(AAS),
∴NP=AG=2﹣![]() ,AO=GN=
,AO=GN=![]() ,
,
∴AN=2,
∴点P(2﹣2![]() ,﹣2),
,﹣2),
∴直线OP解析式为:y=![]() x,
x,
联立方程组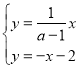
∴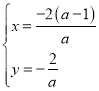
∴点H的纵坐标为![]() ,
,
∴点E(![]() ,
,![]() )
)
∵反比例函数y=![]() 的图象过点E,
的图象过点E,
∴k=![]() ×(
×(![]() )=2,
)=2,
∴反比例函数解析式为:y=![]() ,
,
故答案为:y=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,等边三角形![]() 中,D为
中,D为![]() 边上一点,满足
边上一点,满足![]() ,连接
,连接![]() ,以点A为中心,将射线
,以点A为中心,将射线![]() 顺时针旋转60°,与
顺时针旋转60°,与![]() 的外角平分线
的外角平分线![]() 交于点E.
交于点E.
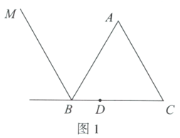
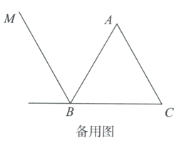
(1)依题意补全图1;
(2)求证:![]() ;
;
(3)若点B关于直线![]() 的对称点为F,连接
的对称点为F,连接![]() .
.
①求证:![]() ;
;
②若![]() 成立,直接写出
成立,直接写出![]() 的度数为_________°.
的度数为_________°.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ;
;
①如图![]() ,若
,若![]() ,且点
,且点![]() 是
是![]() 中点,求证
中点,求证![]() ;
;
②如图![]() ,若
,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,当
,当![]() ,
,![]() 时,点
时,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,当点
,当点![]() 到
到![]() 时两点都停止运动,则点
时两点都停止运动,则点![]() 的运动时间
的运动时间![]() 为多少时,
为多少时,![]() 的面积
的面积![]() 最小,最小面积为多少?
最小,最小面积为多少?
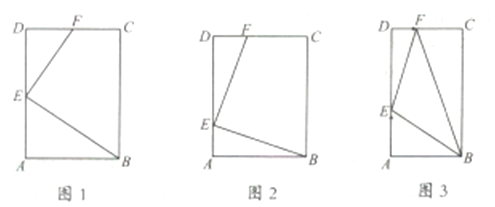
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,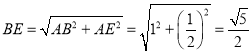 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
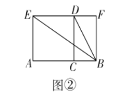
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
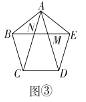
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:小明为了计算![]() 的值 ,采用以下方法:
的值 ,采用以下方法:
设![]() ①
①
则![]() ②
②
②-①得 ![]()
∴![]()
(1)![]() = ;
= ;
(2)![]() = ;
= ;
(3)求![]() 的和(
的和(![]() ,
,![]() 是正整数,请写出计算过程 ).
是正整数,请写出计算过程 ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市为了扎实推进精准扶贫工作,出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A,B,C,D类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成如图两幅不完整的统计图.请根据图中信息,回答下列问题:
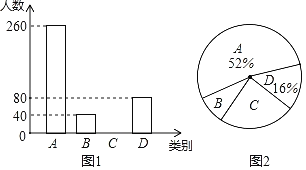
(1)本次抽样调查了多少户贫困户?
(2)成都市共有9100户贫困户,请估计至少得到4种帮扶措施的大约有多少户?
(3)2020年是精准扶贫攻关年,为更好地做好工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行试点帮扶,请用树状图或列表法求出恰好选中乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两家草莓采摘园,草莓的销售价格相间,在生长旺季,两家均排出优惠方案.甲园的优惠方案是:采摘的草莓不超过![]() 时,按原价销售;若超过
时,按原价销售;若超过![]() 超过部分
超过部分![]() 折优惠;乙园的优惠方案是:游客进园需购买
折优惠;乙园的优惠方案是:游客进园需购买![]() 元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓
元门票.采摘的草莓直接按降价出售.已知在甲园、乙园采摘草莓![]() 时,所需费用相同.
时,所需费用相同.
在乙采摘园所需费用![]() ( 元)与草梅采摘量
( 元)与草梅采摘量![]() (千克)满足一次函数关系,如下表:
(千克)满足一次函数关系,如下表:
数量 |
|
|
|
| ··· |
费用 |
|
|
|
| ··· |
(1)求![]() 与
与![]() 的函数关系式(不必写出
的函数关系式(不必写出![]() 的范围);
的范围);
(2)求两个采摘园的草莓在生长旺季前的销售价格.并求在甲采摘园所需费用![]() (元)与草莓采摘量
(元)与草莓采摘量![]() (千克)的函数关系式
(千克)的函数关系式![]() ;
;
(3)若嘉琪准备花费![]() 元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
元去采摘草莓,去哪个园采摘,可以得到更多数量的草莓? 说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A,B两种型号的机器人搬运材料.已知A型机器人比B型机器人每小时多搬运30kg材料,且A型机器人搬运1000kg材料所用的时间与B型机器人搬运800kg材料所用的时间相同.
(1)求A,B两种型号的机器人每小时分别搬运多少材料;
(2)该公司计划采购A,B两种型号的机器人共20台,要求每小时搬运材料不得少于2800kg,则至少购进A型机器人多少台?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com