
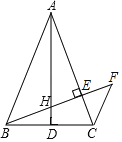
【题目】如图,在△ABC中,AB=AC,AD是边BC上的中线,BE⊥AC于点E,交AD于点H过点C作CF∥AB交BE的延长线于点F.
(1)求证:△ABH∽△BFC;
(2)求证:BH2=HEHF;
(3)若AB=2,∠BAC=45°,求BH的长.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)根据两角对应相等两三角形相似证明即可;
(2)连接CH,首先证明BH=HC,再证明△CHE∽△FHC可得结论;
(3)延长CH交AB于M,由题意CM⊥AB.利用全等三角形的性质证明AM=AE=2,求出BM即可解决问题.
(1)证明:∵AB=AC,AD是边BC上的中线,
∴∠BAD=∠CAD,AD⊥BC,
∵BE⊥AC,
∴∠BDH=∠AEH=90°,
∵∠AHE=∠BHD,
∴∠DBH=∠DAC=∠BAD,
∵CF∥AB,
∴∠ABH=∠F,
∴△ABH∽△BFC;
(2)连接CH.∵AD⊥BC,BD=DC,
∴BH=HC,
∴∠HBC=∠HCB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABH=∠ACH,
∵CF∥AB,
∴∠ABH=∠F,
∴∠HCE=∠F,
∵∠CHE=∠CHF,
∴△CHE∽△FHC,
∴![]() ,
,
∴HC2=HEHF,
∵BH=HC,
∴BH2=HEHF;
(3)延长CH交AB于M,由题意CM⊥AB,

∵BE⊥AC,∠BAC=45°,
∴∠ABE=45°,
∴AE=ABcos45°=2×![]() =
=![]() ,
,
∵∠HAM=∠HAE,∠HMA=∠HEA,∠AMH=∠AEH=90°,
∴△AHM≌△AHE(AAS),
∴AM=AE=![]() ,
,
∴BM=AB﹣AM=2﹣![]() ,
,
在Rt△BHM中,BH=![]() =2
=2![]() ﹣2.
﹣2.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,以BC为直径作半圆O,以点D为圆心、DA为半径做圆弧交半圆O于点P.连结DP并延长交AB于点E.
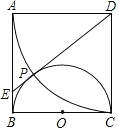
(1)求证:DE为半圆O的切线;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年新型冠状病毒肆虐全球,某地区有一外来无症状感染者,没有有效隔离,经过两轮传染后共有121人患了流感.
(1)每轮传染中平均一个人传染了多少个人?
(2)如果不及时控制,第三轮将又有多少人被传染?
查看答案和解析>>
科目:初中数学 来源: 题型:
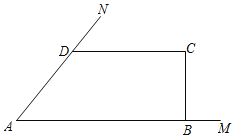
【题目】某市政府为了扶贫,鼓励当地农民养殖小龙虾,如图:张叔叔顺着圩梗AN、AM(AN=3![]() m,AM=10m,∠MAN=45°),用8m长的渔网搭建了一个养殖水域(即四边形ABCD),圩梗边不需要渔网,AB∥CD,∠C=90°.设BC=xm,四边形ABCD面积为S(m2).
m,AM=10m,∠MAN=45°),用8m长的渔网搭建了一个养殖水域(即四边形ABCD),圩梗边不需要渔网,AB∥CD,∠C=90°.设BC=xm,四边形ABCD面积为S(m2).
(1)求出S关于x的函数表达式及x的取值范围;
(2)x为何值时,围成的养殖水域面积最大?最大面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
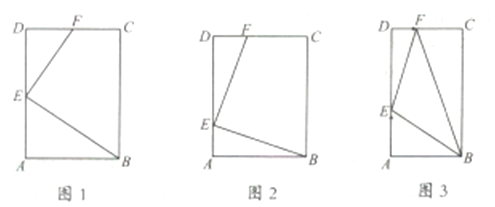
【题目】矩形![]() 中,
中,![]() (其中
(其中![]() )
)
(1)点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,
上,![]() ;
;
①如图![]() ,若
,若![]() ,且点
,且点![]() 是
是![]() 中点,求证
中点,求证![]() ;
;
②如图![]() ,若
,若![]() ,且
,且![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,当
,当![]() ,
,![]() 时,点
时,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,点
,点![]() 以
以![]() 的速度从
的速度从![]() 到
到![]() ,当点
,当点![]() 到
到![]() 时两点都停止运动,则点
时两点都停止运动,则点![]() 的运动时间
的运动时间![]() 为多少时,
为多少时,![]() 的面积
的面积![]() 最小,最小面积为多少?
最小,最小面积为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情爆发以来,口罩成为需求最为迫切的防护物资.在这个关键时刻,我国某企业利用自身优势转产口罩,这背后不仅体现出企业强烈的社会责任感,更是我国人民团结一心抗击疫情的决心.据悉该企业3月份的口罩日产能已达到500万只,预计今后数月内都将保持同样的产能,则3月份(按31天计算)该企业生产的口罩总数量用科学记数法表示为( )
A.![]() 只B.
只B.![]() 只C.
只C.![]() 只D.
只D.![]() 只
只
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应任务:
黄金分割
天文学家开普勒把黄金分割称为神圣分割,并指出毕达哥拉斯定理(勾股定理)和黄金分割是几何中的双宝,前者好比黄金,后者堪称珠宝,历史上最早正式在书中使用“黄金分割”这个名称的是欧姆,19世纪以后“黄金分割”的说法逐渐流行起来,黄金分割被广泛应用于建筑等领域.黄金分割指把一条线段分为两部分,使其中较长部分与线段总长之比等于较短部分与较长部分之比,该比值为![]() .用下面的方法(如图①)就可以作出已知线段
.用下面的方法(如图①)就可以作出已知线段![]() 的黄金分割点
的黄金分割点![]() :
:

①以线段![]() 为边作正方形
为边作正方形![]() ,
,
②取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
③延长![]() 到
到![]() ,使
,使![]() ,
,
④以线段![]() 为边作正方形
为边作正方形![]() ,点
,点![]() 就是线段
就是线段![]() 的黄金分割点.
的黄金分割点.
以下是证明点![]() 就是线段
就是线段![]() 的黄金分割点的部分过程:
的黄金分割点的部分过程:
证明:设正方形![]() 的边长为1,则
的边长为1,则![]() ,
,
![]() 为
为![]() 中点,
中点,
![]() ,
,
![]() 在
在![]() 中,
中,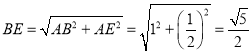 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
…
任务:
(1)补全题中的证明过程;
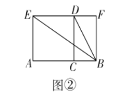
(2)如图②,点![]() 为线段
为线段![]() 的黄金分割点,分别以
的黄金分割点,分别以![]() 为边在线段
为边在线段![]() 同侧作正方形
同侧作正方形![]() 和矩形
和矩形![]() ,连接
,连接![]() .求证:
.求证:![]() ;
;
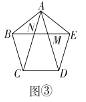
(3)如图③,在正五边形![]() 中,对角线
中,对角线![]() 与
与![]() 分别交于点
分别交于点![]() 求证:点
求证:点![]() 是
是![]() 的黄金分割点.
的黄金分割点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】成都市为了扎实推进精准扶贫工作,出台了民生兜底、医保脱贫、教育救助、产业扶持、养老托管和易地搬迁这六种帮扶措施,每户贫困户都享受了2到5种帮扶措施,现把享受了2种、3种、4种和5种帮扶措施的贫困户分别称为A,B,C,D类贫困户,为检查帮扶措施是否落实,随机抽取了若干贫困户进行调查,现将收集的数据绘制成如图两幅不完整的统计图.请根据图中信息,回答下列问题:
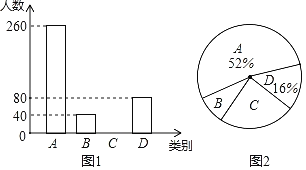
(1)本次抽样调查了多少户贫困户?
(2)成都市共有9100户贫困户,请估计至少得到4种帮扶措施的大约有多少户?
(3)2020年是精准扶贫攻关年,为更好地做好工作,现准备从D类贫困户中的甲、乙、丙、丁四户中随机选取两户进行试点帮扶,请用树状图或列表法求出恰好选中乙和丙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
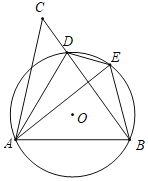
【题目】如图,D是△ABC的BC边上一点,连接AD,作△ABD的外接圆,将△ADC沿直线AD折叠,点C的对应点E落在⊙O上.
(1)求证:AE=AB.
(2)填空:
①当∠CAB=90°,cos∠ADB=![]() ,BE=2时,边BC的长为 .
,BE=2时,边BC的长为 .
②当∠BAE= 时,四边形AOED是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com