
【题目】如图,在正方形ABCD中,以BC为直径作半圆O,以点D为圆心、DA为半径做圆弧交半圆O于点P.连结DP并延长交AB于点E.
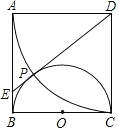
(1)求证:DE为半圆O的切线;
(2)求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据SSS证得△ODP≌△ODC,从而证得∠OPD=∠OCD=90°,即可证得结论;
(2)根据切线长定理和相似三角形的判定与性质得到:(AB﹣EB)2=EB(2AB+EB),整理得到AB=4EB,即可证得AE=3EB,从而求得![]()
(1)证明:连接OP,OD,
∵BC是⊙O的直径,
∴OP=OC,
∵以点D为圆心、DA为半径做圆弧,
∴PD=CD,
在△ODP和△ODC中,
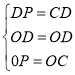 ,
,
∴△ODP≌△ODC(SSS),
∴∠OPD=∠OCD=90°,
∵P点在⊙O上,
∴DE为半圆O的切线;
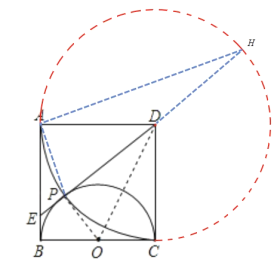
(2)解:∵以点D为圆心、DA为半径做圆,延长ED与圆的另一个交点为H,连接AP,
四边形ABCD是正方形,
∴EA是⊙D的切线,
![]()
![]()
![]() 为圆D的直径,
为圆D的直径,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
∴EA2=EPEH,
同理,EB是半圆O的切线,
∵DE为半圆O的切线,
∴EB=EP,
∵AD=PD=AB,
∴(AB﹣EB)2=EP(PH+EP)
∴(AB﹣EB)2=EB(2AB+EB)
整理得AB=4EB,
∴AE=3EB,
∴![]() .
.


科目:初中数学 来源: 题型:
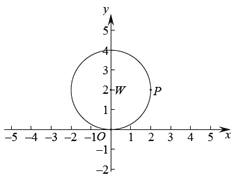
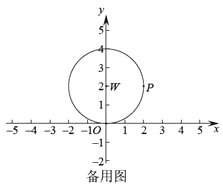
【题目】如图,在平面直角坐标系![]() 中,存在半径为2,圆心为(0,2)的
中,存在半径为2,圆心为(0,2)的![]() ,点
,点![]() 为
为![]() 上的任意一点,线段
上的任意一点,线段![]() 绕点
绕点![]() 逆时针旋转90°得到线段
逆时针旋转90°得到线段![]() ,如果点
,如果点![]() 在线段
在线段![]() 上,那么称点
上,那么称点![]() 为
为![]() 的“限距点”.
的“限距点”.
(1)在点![]() 中,
中,![]() 的“限距点”为____________________________;
的“限距点”为____________________________;
(2)如果过点![]() 且平行于
且平行于![]() 轴的直线
轴的直线![]() 上始终存在
上始终存在![]() 的“限距点”,画出示意图并直接写出
的“限距点”,画出示意图并直接写出![]() 的取值范围;
的取值范围;
(3)![]() 的圆心为
的圆心为![]() ,半径为1,如果
,半径为1,如果![]() 上始终存在
上始终存在![]() 的“限距点”,请直接写出
的“限距点”,请直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学进校时需要从学校大门A、B、C三个入口处中的任意一处测量体温,体温正常方可进校.
(1)甲同学在A入口处测量体温的概率是 ;
(2)求甲、乙两位同学在同一入口处测量体温的概率.(用“画树状图”或“列表”的方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校与图书馆在同一条笔直道路上,甲从学校去图书馆,乙从图书馆回学校,甲、乙两人都匀速步行且同时出发,乙先到达目的地.两人之间的距离y(米)与时间t(分钟)之间的函数关系如图所示.乙回到学校用了______分钟.
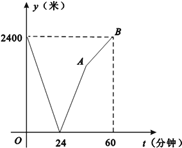
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.
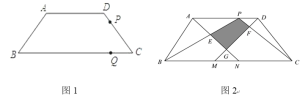
(1)梯形ABCD的面积等于 .
(2)如图1,动点P从D点出发沿DC以DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.当PQ∥AB时,P点离开D点多少时间?
(3)如图2,点K是线段AD上的点,M、N为边BC上的点,BM=CN=5,连接AN、DM,分别交BK、CK于点E、F,记△ ADG和△ BKC重叠部分的面积为S,求S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织了2000名学生参加“爱我中华”知识竞赛活动,为了了解本次知识竞赛的成绩分布情况,从中抽取了部分学生的得分进行统计:
成绩 | 频数 | 频率 |
| 20 |
|
| 16 | 0.08 |
|
| 0.15 |
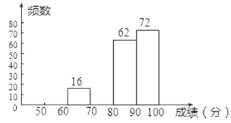
请你根据以上的信息,回答下列问题:
(1)![]() ,
,![]() ;
;
(2)在扇形统计图中,“成绩![]() 满足
满足![]() ”对应扇形的圆心角的度数是 ;
”对应扇形的圆心角的度数是 ;
(3)若将得分转化为等级,规定:![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() ,
,![]() 评为
评为![]() .这次全校参加竞赛的学生约有 人参赛成绩被评为“
.这次全校参加竞赛的学生约有 人参赛成绩被评为“![]() ”.
”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,正方形
中,正方形![]() 的边长为2,函数
的边长为2,函数![]() 的图象经过点B,与直线
的图象经过点B,与直线![]() 交于点D.
交于点D.
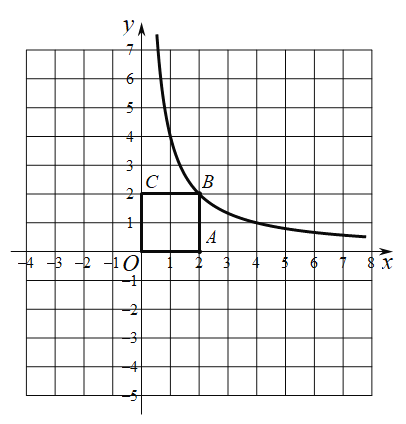
(1)求k的值;
(2)直线![]() 与
与![]() 边所在直线交于点M,与x轴交于点N.
边所在直线交于点M,与x轴交于点N.
①当点D为![]() 中点时,求b的值;
中点时,求b的值;
②当![]() 时,结合函数图象,直接写出b的取值范围.
时,结合函数图象,直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD是边BC上的中线,BE⊥AC于点E,交AD于点H过点C作CF∥AB交BE的延长线于点F.
(1)求证:△ABH∽△BFC;
(2)求证:BH2=HEHF;
(3)若AB=2,∠BAC=45°,求BH的长.
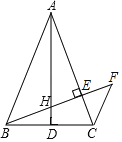
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com