
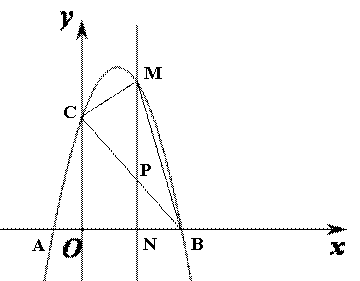
如图,已知抛物线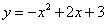 与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,连接BC。
(1)求A、B、C三点的坐标;
(2)若点P为线段BC上的一点(不与B、C重合),PM∥y轴,且PM交抛物线于点M,交x轴于点N,当△BCM的面积最大时,求△BPN的周长;
(3)在(2)的条件下,当BCM的面积最大时,在抛物线的对称轴上存在点Q,使得△CNQ为直角三角形,求点Q的坐标。
解:(1)令x=0,解得y=3
 ∴点C的坐标为(0,3)
∴点C的坐标为(0,3)
令y=0,解得x1=-1,x2=3
∴点A的坐标为(-1,0)
点B的坐标为(3,0)
(2)由A,B两点坐标求得直线AB的解析式为y=-x+3
设点P的坐标为(x,-x+3)(0<x<3)
∵PM∥y轴
∠PNB=90°,点M的坐标为(x,-x2+2x+3)
∴PM=(-x2+2x+3)-(-x+3)
=-x2+3x
∵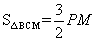
∴当x=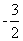 时
时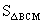 的面积最大
的面积最大
 此时,点P的坐标为(
此时,点P的坐标为(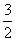 ,
,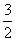 )
)
∴PN=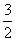 ,BN=
,BN=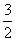 ,BP=
,BP=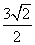
∴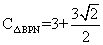 .
.
(3)求得抛物线对称轴为x=1
设点Q的坐标为(1,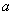 )
)
 ∴
∴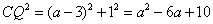
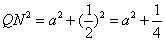
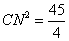
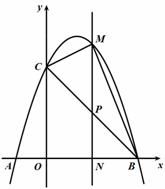
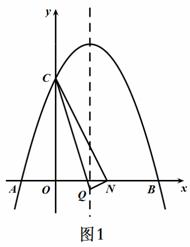
① 当∠CNQ=90°时, 如图1所示
即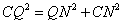
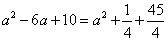
解得: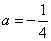
∴Q1(1,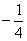 )
)
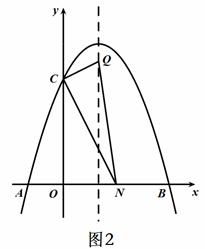
② 当∠NCQ=90°时,如图2所示
即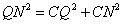

 解得:
解得: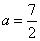
∴Q2(1,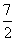 )
)
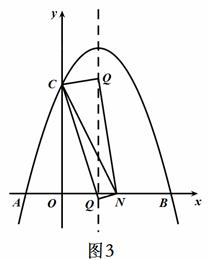
③ 当∠CQN=90°时,如图3所示
即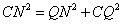
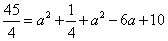
解得: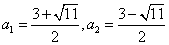
∴Q3(1,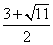 )Q4(1,
)Q4(1,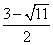 )
)


科目:初中数学 来源: 题型:
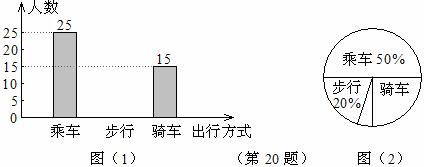
学了统计知识后,小刚就本班同学上学“喜欢的出行方式”进行了一次调查。图(1)和图(2)是他根据采集的数据绘制的两幅不完整的统计图,请根据图中提供的信息解答以下问题:
(1)补 全条形统计图,并计算出“骑车”部分所对应的圆心角的度数;
全条形统计图,并计算出“骑车”部分所对应的圆心角的度数;
(2)如果全年级共600名同学,请估算全年级步行上学的学生人数;
(3)若由3名“喜欢乘车”的学生,1名“喜欢步行”的学生,1名“喜欢骑车”的学生组队参加一项活动,欲从中选出2人担任组长(不分正副),列出所有可能的情况,并求出2人都是“喜欢乘车”的学生的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
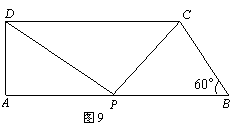
如图9,在直角梯形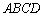 中,
中,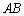 ∥
∥ ,
,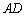 ⊥
⊥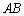 ,
,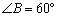 ,
,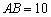 ,
,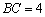 ,
,
点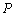 沿线段
沿线段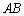 从点
从点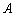 向点
向点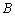 运动,设
运动,设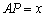 .
.
(1)求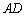 的长;
的长;
(2)点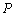 在运动过程中,是否存在以
在运动过程中,是否存在以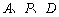 为顶点的三角形与以
为顶点的三角形与以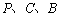 为顶点的三角形相似?若存在,求出
为顶点的三角形相似?若存在,求出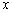 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设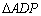 与
与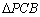 的外接圆的面积分别为
的外接圆的面积分别为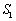 、
、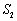 ,若
,若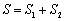 ,求
,求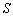 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com