
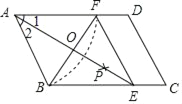
����Ŀ����ͼ����ABCD�У��Ե�AΪԲ�ģ�AB��Ϊ�뾶������AD�ڵ�F���ٷֱ��Ե�B��FΪԲ�ģ�����![]() BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
BF�ij�Ϊ�뾶��������������һ��P������AP���ӳ���BC�ڵ�E������EF��
��1��������������ͼ��Ϣ֪�ı���ABEF���� ��
A���������ƽ���ı���
B������
C������
D��������
��2����AE��BF�ཻ�ڵ�O���ı���ABEF���ܳ�Ϊ16��BF=4����AE�ij��͡�C�Ķ�����
���𰸡���1��C����2��60��
��������
��1��������ͼ����֪����ȷ�����ı���ABEF����״���ɣ�
��2������������������BE�ij������ù��ɶ������OE�ij����̶����AE�ij����õ�������BEFΪ�ȱ������Σ�������ƽ���ı��ε����ʼ����������
��1��������������ͼ��Ϣ֪�ı���ABEF�����Σ�
��ѡC��
��2�����ı���ABEF�����Σ�
��AE��BF��OB=OF��
��BF=4��
��![]()
���ı���ABEF���ܳ�Ϊ16��
��BE=4��
��Rt��OBE�У����ݹ��ɶ����ã�![]()
��![]()
��BE=BF=EF=4��
���BEF�ǵȱ������Σ�
���FEB=60�㣬
���ı���ABCD��ƽ���ı��Σ�
��AB��EF��
��AB��CD��
��CD��EF��
���C=��BEF=60�㣮


 �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д� һ���㶨ϵ�д�
һ���㶨ϵ�д� ��У��ҵ��ϵ�д�
��У��ҵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB��AC����E�ڡ�ABC��һ�㣬CE��AE�ڵ�E��CE��![]() BC��
BC��
��1��������ABC�Ľ�ƽ����AD����Ҫ�߹���ͼ����д������������ͼ�ۼ�����
��2����֤����ACE����B��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ģ���֪���κ���![]() ��ͼ����һ�κ���
��ͼ����һ�κ���![]() ��ͼ���ཻ��
��ͼ���ཻ��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ��ֵӦ������ ��
��ֵӦ������ ��
A. -3<x1<-2 B. -2<x1<-1 C. -1<x1<0 D. 0<x1<1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪ѧϰ��
���һ����������һ���ϵ����ߵ��������ߵ�һ�룬��ô���ǾͰ������������ν������ǻ������Ρ���
�������ã�
��1���������������Σ����ǻ������ε���______������ţ���

��2����ͼ����֪�ȱ�������![]() �����ÿ̶ȳ��ڸ������α����ҳ��������������ĵ�
�����ÿ̶ȳ��ڸ������α����ҳ��������������ĵ�![]() ��ʹ
��ʹ![]() Ϊ���ǻ������Ρ�����д��������
Ϊ���ǻ������Ρ�����д��������

������̽����
��3����ͼ����������![]() �У���
����![]() ��
��![]() ���е㣬
���е㣬![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() �����ж�
�����ж�![]() �Ƿ�Ϊ���ǻ������Ρ�����˵�����ɣ�
�Ƿ�Ϊ���ǻ������Ρ�����˵�����ɣ�

�����Ӧ�ã�
��4����ͼ���ȱ�������![]() �߳�
�߳�![]() ��������
��������![]() ��
��![]() ���ٶȴӵ�
���ٶȴӵ�![]() ��������
��������![]() �ı�
�ı�![]() �˶�������һ����
�˶�������һ����![]() ��
��![]() ���ٶȴӵ�
���ٶȴӵ�![]() �������ر�
�������ر�![]() �˶�������ͬʱ����������
�˶�������ͬʱ����������![]() �״λص���
�״λص���![]() ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊ
ʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊ![]() ����ô
����ô![]() Ϊ______
Ϊ______![]() ʱ��
ʱ��![]() Ϊ���ǻ������Ρ���
Ϊ���ǻ������Ρ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c����A����5��0����B��1��0����C��0��![]() ������
������
��1����գ������ߵĽ���ʽ��������
��2�����������ߵĶԳ�������һ��P��ʹPB+PC��ֵ��С�����P�����ꣻ
�ڵ�MΪx����һ���㣬�����������Ƿ����һ��N��ʹ��B��C��M��N�ĵ㹹�ɵ��ı���Ϊƽ���ı��Σ������ڣ����N�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
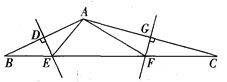
����Ŀ����ͼ����ABC�У�AB��AC�Ĵ�ֱƽ���߷ֱ�BC�ڵ�E��F������AEF���ܳ�Ϊ12cm����BC�ij�Ϊ____________________cm������EAF=110�������BAC��_____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,�ڡ�ABC�У���D�ڱ�AC�ϣ����������У����жϡ�BDC���ABC���Ƶ��� ( )

A. AB��CB=CA��CD B. AB��CD=BD��BC C. BC2=AC��DC D. BD2=CD��DA
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������߲��ŵ�Ҫ����Ӿ�ر��붨�ڻ�ˮ����ܶ���ţ��ڻ�ˮʱ��Ҫ������ˮ����������ˮ���Ĺ��̣�ij��Ӿ�ݴ�����7��00��ʼ����Ӿ�ؽ��л�ˮ����֪����Ӿ�ص���ˮ�ٶ��ǹ�ˮ�ٶȵ�1.6����������Ӿ����ʣ���ˮ��y(m3)�뻻ˮʱ��x(h)֮��ĺ���ͼ����ͼ��ʾ������ͼ�����������⣺
(1)��գ�����Ӿ����ϴ��Ҫ�� ��Сʱ��
(2)����ˮ�����е�y(m3)��x(h)֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
(3)������Ӿ���ڻ�ˮ������30���Ӳ��ܶ���ţ�������Ӿ������С���ܷ�������12��40�������Ӿ����Ӿ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
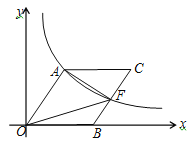
����Ŀ����ͼ,OΪ����ԭ��,��B��x�����������,�ı���OACB��ƽ���ı���,OA =10��sin��AOB =![]() ,����������y =kx-1(k>0)�ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F.
,����������y =kx-1(k>0)�ڵ�һ�����ڵ�ͼ����A����BC���ڵ�F.
(1)���������ı���ʽ��
(2)����FΪBC���е㣬����OBF�����.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com