
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD
(1)求证:BD平分∠ABC;
(2)当∠ODB=30°时,求证:BC=OD.
【答案】
(1)
∵OD⊥AC OD为半径,∴ ![]() ,
,
∴∠CBD=∠ABD,
∴BD平分∠ABC;
(2)
证明:∵OB=OD,
∴∠OBD=∠0DB=30°,
∴∠AOD=∠OBD+∠ODB=30°+30°=60°,
又∵OD⊥AC于E,
∴∠OEA=90°,
∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°,
又∵AB为⊙O的直径,
∴∠ACB=90°,
在Rt△ACB中,BC= ![]() AB,
AB,
∵OD= ![]() AB,
AB,
∴BC=OD
【解析】(1)由OD⊥AC OD为半径,根据垂径定理,即可得 ![]() ,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.
,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可证得BD平分∠ABC;(2)首先由OB=OD,易求得∠AOD的度数,又由OD⊥AC于E,可求得∠A的度数,然后由AB是⊙O的直径,根据圆周角定理,可得∠ACB=90°,继而可证得BC=OD.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,直线![]() ,
,![]() ,
,![]() 分别通过A,B,C三点,且
分别通过A,B,C三点,且![]() ,若
,若![]() 与
与![]() 的距离为5,
的距离为5,![]() 与
与![]() 的距离为7,则正方形ABCD的面积等于( )
的距离为7,则正方形ABCD的面积等于( )

A. 148 B. 70 C. 144 D. 74
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丁将中国的清华大学、北京大学及英国的剑桥大学的图片分别贴在3张完全相同的不透明的硬纸板上,制成名校卡片,如图,小丁将这3张卡片背面朝上洗匀后放在桌子上,从中随机取一张卡片,放回后洗匀,在随机抽取一张卡片.
(1)小丁第一次抽取的卡片上的图片是剑桥大学的概率是多少?(请直接写出结果)
(2)请你用列表法或画树状图(树状图)法,帮助小丁求出两次抽取的卡片上的图片一个是国内大学,一个是国外大学的概率.(卡片名称可用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线y=﹣2x+4与两坐标轴分别交于点A、B,点C为线段OA上一动点,连接BC,作BC的中垂线分别交OB、AB交于点D、E.
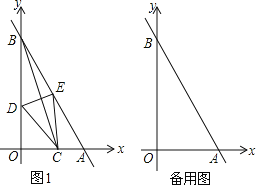
(l)当点C与点O重合时,DE= ;
(2)当CE∥OB时,证明此时四边形BDCE为菱形;
(3)在点C的运动过程中,直接写出OD的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com