
 如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE.且点G在矩形ABCD内部.如果将BG延长交DC于点F.
如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE.且点G在矩形ABCD内部.如果将BG延长交DC于点F.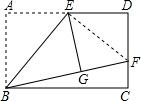 则根据翻折不变性得,
则根据翻折不变性得,
|


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| A、(1)(2)(4) |
| B、(3)(4) |
| C、(2)(3) |
| D、(2)(4) |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 1 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
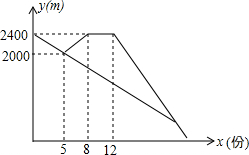 小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题.
小明和爸爸从家一起出发,沿相同的路线以相同的速度步行去体育馆看球赛,途中发现忘带球票,小明立即以更快的速度跑步返回家取票,爸爸继续以原来的速度步行前往体育馆.小明上楼取票用了几分钟后骑自行车沿原来的路线骑向体育馆,小明追上爸爸后用自行车带着爸爸一起前往体育馆,自行车的速度是出发时步行速度的3倍.如图是小明和爸爸距体育馆的路程y(米)与出发的时间x(分)的函数图象.根据图象解答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:
 一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.
一家用电器开发公司研制出一种新型电子产品,每件的生产成本为18元,按定价40元出售,每月可销售20万件.为了增加销量,公司决定采取降价的办法,经市场调研,每降价1元,月销售量可增加2万件.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com