
ЁОЬтФПЁПФГОЯњЩЬЯњЪлвЛжжВњЦЗЃЌетжжВњЦЗЕФГЩБОМлЮЊ10дЊ/ЧЇПЫЃЌвбжЊЯњЪлМлВЛЕЭгкГЩБОМлЃЌЧвЮяМлВПУХЙцЖЈетжжВњЦЗЕФЯњЪлМлВЛИпгк18дЊ/ЧЇПЫЃЌЪаГЁЕїВщЗЂЯжЃЌИУВњЦЗУПЬьЕФЯњЪлСПyЃЈЧЇПЫЃЉгыЯњЪлМлxЃЈдЊ/ЧЇПЫЃЉжЎМфЕФКЏЪ§ЙиЯЕШчЭМЫљЪОЃК
ЃЈ1ЃЉЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓУПЬьЕФЯњЪлРћШѓWЃЈдЊЃЉгыЯњЪлМлxЃЈдЊ/ЧЇПЫЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎЕБЯњЪлМлЮЊЖрЩйЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉИУОЯњЩЬЯывЊУПЬьЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлМлгІЖЈЮЊЖрЩйЃП

ЁОД№АИЁПЃЈ1ЃЉy=-2x+60ЃЈ10ЁмxЁм18ЃЉЃЛЃЈ2ЃЉЯњЪлМлЮЊ18дЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ192дЊЃЎЃЈ3ЃЉ15дЊЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉЩшКЏЪ§ЙиЯЕЪНy=kx+bЃЌАбЃЈ10ЃЌ40ЃЉЃЌЃЈ18ЃЌ24ЃЉДњШыЧѓГіkКЭbМДПЩЃЌгЩГЩБОМлЮЊ10дЊ/ЧЇПЫЃЌЯњЪлМлВЛИпгк18дЊ/ЧЇПЫЃЌЕУГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉИљОнЯњЪлРћШѓ=ЯњЪлСПЁСУПвЛМўЕФЯњЪлРћШѓЕУЕНwКЭxЕФЙиЯЕЃЌРћгУЖўДЮКЏЪ§ЕФаджЪЕУзюжЕМДПЩЃЛ
ЃЈ3ЃЉЯШАбy=150ДњШыЃЈ2ЃЉЕФКЏЪ§ЙиЯЕЪНжаЃЌНтвЛдЊЖўДЮЗНГЬЧѓГіxЃЌдйИљОнxЕФШЁжЕЗЖЮЇМДПЩШЗЖЈxЕФжЕЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЩшyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНy=kx+bЃЌАбЃЈ10ЃЌ40ЃЉЃЌЃЈ18ЃЌ24ЃЉДњШыЕУ
![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЌ
ЃЌ
ЁрyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНy=-2x+60ЃЈ10ЁмxЁм18ЃЉЃЛ
ЃЈ2ЃЉW=ЃЈx-10ЃЉЃЈ-2x+60ЃЉ
=-2x2+80x-600ЃЌ
ЖдГЦжсx=20ЃЌдкЖдГЦжсЕФзѓВрyЫцзХxЕФдіДѓЖјдіДѓЃЌ
Ёп10ЁмxЁм18ЃЌ
ЁрЕБx=18ЪБЃЌWзюДѓЃЌзюДѓЮЊ192ЃЎ
МДЕБЯњЪлМлЮЊ18дЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ192дЊЃЎ
ЃЈ3ЃЉгЩ150=-2x2+80x-600ЃЌ
НтЕУx1=15ЃЌx2=25ЃЈВЛКЯЬтвтЃЌЩсШЅЃЉ
Д№ЃКИУОЯњЩЬЯывЊУПЬьЛёЕУ150дЊЕФЯњЪлРћШѓЃЌЯњЪлМлгІЖЈЮЊ15дЊЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() гывЛДЮКЏЪ§
гывЛДЮКЏЪ§![]() ЃЌСю
ЃЌСю![]() .
.
ЃЈ1ЃЉШє![]() ЕФКЏЪ§ЭМЯѓЯрНЛгк
ЕФКЏЪ§ЭМЯѓЯрНЛгк![]() жсЩЯЕФЭЌвЛЕуЃЎ
жсЩЯЕФЭЌвЛЕуЃЎ
ЂйЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФжЕзюаЁЃЌЪдЧѓГіИУзюаЁжЕЃЎ
ЕФжЕзюаЁЃЌЪдЧѓГіИУзюаЁжЕЃЎ
ЃЈ2ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁЃЌЧыаДГі
ЕФдіДѓЖјМѕаЁЃЌЧыаДГі![]() ЕФДѓаЁЙиЯЕВЂИјгшжЄУїЃЎ
ЕФДѓаЁЙиЯЕВЂИјгшжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКШЮвтСНИіЪ§a ЁЂb ЃЌАДЙцдђc = a +bЃab РЉГфЕУЕНвЛИіаТЪ§c ЃЌГЦЫљЕУЕФаТЪ§c ЮЊЁАШчвтЪ§ЁБ.
ЃЈ1ЃЉШєa =2ЃЌ b =Ѓ3ЃЌжБНгаДГіa ЁЂb ЕФЁАШчвтЪ§ЁБ c ЃЛ
ЃЈ2ЃЉШєa =2ЃЌ b = x2 +1ЃЌЧѓa ЁЂb ЕФЁАШчвтЪ§ЁБ c ЃЌВЂБШНЯb гыc ЕФДѓаЁЃЛ
ЃЈ3ЃЉвбжЊa=x2-1ЃЌЧвa ЁЂb ЕФЁАШчвтЪ§ЁБ c = x3 +3x2Ѓ1ЃЌдђb = ЃЈгУКЌ x ЕФЪНзгБэЪОЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌГЌЪаОйаагаНБДйЯњЛюЖЏЃКЗВвЛДЮадЙКЮяТњ300дЊепМДПЩЛёЕУвЛДЮвЁНБЛњЛсЃЌвЁНБЛњЪЧвЛИідВаЮзЊХЬЃЌБЛЗжГЩ16ЕШЗжЃЌжИеыЗжБ№жИЯђКьЁЂЛЦЁЂРЖЩЋЧјгђЃЌЗжЛёвЛЁЂЖўЁЂШ§ЛёНБЃЌНБН№вРДЮЮЊ60ЁЂ50ЁЂ40дЊЃЎ
ЃЈ1ЃЉЗжБ№МЦЫуЛёвЛЁЂЖўЁЂШ§ЕШНБЕФИХТЪЃЎ
ЃЈ2ЃЉРЯРювЛДЮадЙКЮяТњСЫ300дЊЃЌвЁНБвЛДЮЃЌЛёНБЕФИХТЪЪЧЖрЩйЃПЧыФудЄВтвЛЯТРЯРювЁНБНсЙћЛсгаФФМИжжЧщПіЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧОиаЮжНЦЌЃЌ![]() ЖделОиаЮжНЦЌABCDЃЌЪЙADгыBCжиКЯелКлЮЊEFЃЛеЙЦНКѓдйЙ§ЕуBелЕўОиаЮжНЦЌЃЌЪЙЕуAТфдкEFЩЯЕФЕуNЃЌелКлBMгыEFЯрНЛгкЕуQЃЛдйДЮеЙЦНЃЌСЌНгBNЃЌMNЃЌбгГЄMNНЛBCгкЕу
ЖделОиаЮжНЦЌABCDЃЌЪЙADгыBCжиКЯелКлЮЊEFЃЛеЙЦНКѓдйЙ§ЕуBелЕўОиаЮжНЦЌЃЌЪЙЕуAТфдкEFЩЯЕФЕуNЃЌелКлBMгыEFЯрНЛгкЕуQЃЛдйДЮеЙЦНЃЌСЌНгBNЃЌMNЃЌбгГЄMNНЛBCгкЕу![]() гаШчЯТНсТлЃК
гаШчЯТНсТлЃК![]() ЃЛ
ЃЛ![]() ЪЧЕШБпШ§НЧаЮЃЛ
ЪЧЕШБпШ§НЧаЮЃЛ![]() ЃЛ
ЃЛ![]() ЮЊЯпЖЮBMЩЯвЛЖЏЕуЃЌHЪЧBNЕФжаЕуЃЌдђ
ЮЊЯпЖЮBMЩЯвЛЖЏЕуЃЌHЪЧBNЕФжаЕуЃЌдђ![]() ЕФзюаЁжЕЪЧ
ЕФзюаЁжЕЪЧ![]() Цфжае§ШЗНсТлЕФИіЪ§ЪЧ
Цфжае§ШЗНсТлЕФИіЪ§ЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁППЮБОЁАФПБъгыЦРЖЈЁБжагаетбљвЛЕРЫМПМЬтЃКШчЭМИжМмжаЁЯA=20ЁуЃЌКИЩЯЕШБпЕФИжЬѕP1P2ЃЌP2P3ЃЌP3P4ЃЌP4P5ЁРДМгЙЬИжМмЃЌШєP1A=P1P2ЃЌЮЪетбљЕФИжЬѕжСЖрашвЊЖрЩйИљЃП
ЃЈ1ЃЉЧыНЋЯТСаНтД№Й§ГЬВЙГфЭъећЃК
Д№АИЃКЁпЁЯA=20ЁуЃЌP1A=P1P2ЃЌЁрЁЯP1P2A=ЁЁ ЁЁ.
гжP1P2=P2P3=P3P4=P4P5ЃЌЁрЁЯP2P1P3=P2P3P1=40ЁуЃЌ
ЭЌРэПЩЕУЃЌЁЯP3P2P4=P3P4P2=60ЁуЃЌЁЯP4P3P5=P4P5P3=ЁЁ ЁЁЃЌ
ЁрЁЯBP4P5=ЁЯCP5P4=100ЁуЃО90ЁуЃЌ
ЁрЖдгкЩфЯпP4BЩЯШЮвтвЛЕуP6ЃЈЕуP4Г§ЭтЃЉЃЌP4P5ЃМP5P6ЃЌ
ЁретбљЕФИжМмжСЖрашвЊЁЁ ЁЁИљ.
ЃЈ2ЃЉМЬајЬНОПЃКЕБЁЯA=15ЁуЪБЃЌетбљЕФИжЬѕжСЖрашвЊЖрЩйИљЃП
ЃЈ3ЃЉЕБетбљЕФИжЬѕжСЖрашвЊ8ИљЪБЃЌЬНОПЁЯAЕФШЁжЕЗЖЮЇ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЪЬтЧщОГ
аЁУїКЭаЁРіЙВЭЌЬНОПвЛЕРЪ§бЇЬтЃК
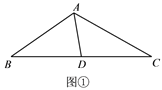
ШчЭМЂйЃЌдкЁїABCжаЃЌЕуDЪЧБпBCЕФжаЕуЃЌЁЯBAD=65ЁуЃЌЁЯDAC=50ЁуЃЌAD=2ЃЌ
ЧѓACЃЎ
ЬНЫїЗЂЯж
аЁУїЕФЫМТЗЪЧЃКбгГЄADжСЕуEЃЌЪЙDE=ADЃЌЙЙдьШЋЕШШ§НЧаЮЃЎ
аЁРіЕФЫМТЗЪЧЃКЙ§ЕуCзїCEЁЮABЃЌНЛADЕФбгГЄЯпгкЕуEЃЌЙЙдьШЋЕШШ§НЧаЮЃЎ
бЁдёаЁУїЁЂаЁРіЦфжавЛШЫЕФЗНЗЈНтОіЮЪЬтЧщОГжаЕФЮЪЬтЃЎ
РрБШгІгУ
ШчЭМЂкЃЌдкЫФБпаЮABCDжаЃЌЖдНЧЯпACЁЂBDЯрНЛгкЕуOЃЌЕуOЪЧBDЕФжаЕуЃЌ

ABЁЭACЃЎШєЁЯCAD=45ЁуЃЌЁЯADC=67.5ЁуЃЌAO=2ЃЌдђBCЕФГЄЮЊ___________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОеаЦИЭтТєЫЭВЭдБЃЌЫЭВЭдБЕФдТЙЄзЪгЩЕзаН1000дЊМгЩЯЭтТєЫЭЕЅВЙЬљ![]() ЫЭвЛДЮЭтТєГЦЮЊвЛЕЅ
ЫЭвЛДЮЭтТєГЦЮЊвЛЕЅ![]() ЙЙГЩЃЌЭтТєЫЭЕЅВЙЬљЕФОпЬхЗНАИШчЯТЃК
ЙЙГЩЃЌЭтТєЫЭЕЅВЙЬљЕФОпЬхЗНАИШчЯТЃК
ЭтТєЫЭЕЅЪ§СП | ВЙЬљ |
УПдТВЛГЌЙ§500ЕЅ | 6 |
ГЌЙ§500ЕЅЕЋВЛГЌЙ§mЕЅЕФВПЗж | 8 |
ГЌЙ§mЕЅЕФВПЗж | 10 |
![]() ШєФГЁАЭтТєаЁИчЁБ4дТЗнЫЭВЭ400ЕЅЃЌдђЫћетИідТЕФЙЄзЪзмЖюЮЊЖрЩйдЊЃП
ШєФГЁАЭтТєаЁИчЁБ4дТЗнЫЭВЭ400ЕЅЃЌдђЫћетИідТЕФЙЄзЪзмЖюЮЊЖрЩйдЊЃП
![]() Щш5дТЗнФГЁАЭтТєаЁИчЁБЫЭВЭxЕЅ
Щш5дТЗнФГЁАЭтТєаЁИчЁБЫЭВЭxЕЅ![]() ЃЌЫљЕУЙЄзЪЮЊyдЊЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЎ
ЃЌЫљЕУЙЄзЪЮЊyдЊЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЎ
![]() ШєФГЁАЭтТєаЁИчЁБ5дТЗнЫЭВЭ800ЕЅЃЌЫљЕУЙЄзЪЮЊ6500дЊЃЌЧѓmЕФжЕЃЎ
ШєФГЁАЭтТєаЁИчЁБ5дТЗнЫЭВЭ800ЕЅЃЌЫљЕУЙЄзЪЮЊ6500дЊЃЌЧѓmЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЛЏМђЧѓжЕЃКвбжЊxЃЌyТњзуЃКx2+y2Љ4x+6y+13ЃН0ЃЎЧѓДњЪ§ЪН[ЃЈ3xЉyЃЉ2Љ4ЃЈ2x+yЃЉЃЈxЉyЃЉЉЃЈxЉ3yЃЉЃЈx+3yЃЉ]ЁТЃЈЉ![]() yЃЉЕФжЕЃЎ
yЃЉЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com