
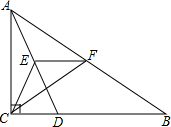
 如图,在△ABC中,∠ACB=90°,点E,F分别是AD,AB中点,AD=BD
如图,在△ABC中,∠ACB=90°,点E,F分别是AD,AB中点,AD=BD分析 (1)根据三角形中位线定理得到EF=$\frac{1}{2}$BD,根据直角三角形的性质得到CE=$\frac{1}{2}$AD,根据题意得到CE=EF;
(2)根据三角形中位线定理、直角三角形的性质求出CE=EF=$\frac{1}{2}$a,CF=$\frac{1}{2}$b,根据周长公式计算即可.
解答 (1)证明:∵点E,F分别是AD,AB中点,
∴EF=$\frac{1}{2}$BD,
∵∠ACB=90°,点E是AD的中点,
∴CE=$\frac{1}{2}$AD,
∵AD=BD,
∴CE=EF,
∴△CEF是等腰三角形;
(2)解:由(1)得,CE=EF=$\frac{1}{2}$AD=$\frac{1}{2}$a,
∵∠ACB=90°,点F是AB中点,
∴CF=$\frac{1}{2}$AB=$\frac{1}{2}$b,
∴△CEF的周长=a+$\frac{1}{2}$b.
点评 本题考查的是三角形中位线定理、直角三角形的性质,掌握三角形的中位线平行于第三边且等于第三边的一半、直角三角形斜边上的中线是斜边的一半是解题的关键.


 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:
设有两个非负数a、b.则有如下证明:∵($\sqrt{a}$-$\sqrt{b}$)2≥0(当且仅当a=b时等号成立).∴a-2$\sqrt{ab}$+b≥0.∴a+b≥2$\sqrt{ab}$,∴$\sqrt{ab}$≤$\frac{a+b}{2}$(或ab≤$\frac{(a+b)^{2}}{4}$)(当且仅当a=b时等号成立)根据这一证明的结论解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 14% | B. | 15% | C. | 16% | D. | 17% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com