
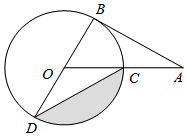
 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )| A. | $\frac{4}{3}π-\sqrt{3}$ | B. | $\frac{4}{3}π-2\sqrt{3}$ | C. | $4π-4\sqrt{3}$ | D. | $\frac{16}{3}π-4\sqrt{3}$ |
分析 过O点作OE⊥CD于E,首先根据切线的性质和直角三角形的性质可得∠AOB=60°,再根据平角的定义和三角形外角的性质可得∠COD=120°,∠OCD=∠ODC=30°,根据含30°的直角三角形的性质可得OE,CD的长,再根据阴影部分的面积=扇形OCD的面积-三角形OCD的面积,列式计算即可求解.
解答 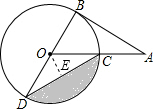 解:如图,过O点作OE⊥CD于E,
解:如图,过O点作OE⊥CD于E,
∵AB为⊙O的切线,
∴∠ABO=90°,
∵∠A=30°,
∴∠AOB=60°,
∴∠COD=120°,∠OCD=∠ODC=30°,
∴OE=$\frac{1}{2}$OD=2,CE=DE=$\frac{\sqrt{3}}{2}$OD=2$\sqrt{3}$,
∴CD=2CE=4$\sqrt{3}$,
∴S阴影=S扇形COD-S△COD=$\frac{120π×{4}^{2}}{360}$-$\frac{1}{2}$×4$\sqrt{3}$×2=$\frac{16π}{3}$-4$\sqrt{3}$,
故选D.
点评 本题主考查了扇形面积的计算,切线的性质,本题关键是理解阴影部分的面积=扇形OCD的面积-三角形OCD的面积.


科目:初中数学 来源: 题型:选择题
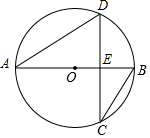 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )| A. | 3$\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $5\sqrt{3}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)
某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
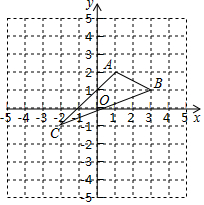 在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com