
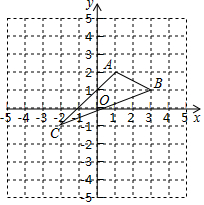
 在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).
在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1). 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:选择题
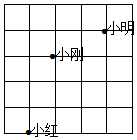 如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )
如图所示是做课间操时,小明、小红、小刚三人的相对位置,如果用(4,5)表示小明的位置,(2,4)表示小刚的位置,则小红的位置可表示为( )| A. | (0,0) | B. | (0,1) | C. | (1,0) | D. | (1,1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 一次性购物 | 优惠办法 |
| 少于200元 | 不予优惠 |
| 低于500元但不低于200元 | 九折优惠 |
| 500元或超过500元 | 其中500元部分给予九折优惠; 超过500元部分给予八折优惠 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
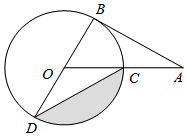 如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )
如图,AB为⊙O的切线,切点为B,连接AO,OA与⊙O交于点C,BD为⊙O的直径,连接CD,若∠A=30°,⊙O的半径为4,则图中阴影部分的面积为( )| A. | $\frac{4}{3}π-\sqrt{3}$ | B. | $\frac{4}{3}π-2\sqrt{3}$ | C. | $4π-4\sqrt{3}$ | D. | $\frac{16}{3}π-4\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com