
【题目】已知抛物线与![]() 轴交于点
轴交于点![]() 和
和![]() 且过点
且过点![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 抛物线的顶点坐标;
抛物线的顶点坐标;
![]()
![]() 取什么值时,
取什么值时,![]() 随
随![]() 的增大而增大;
的增大而增大;![]() 取什么值时,
取什么值时,![]() 随
随![]() 增大而减小.
增大而减小.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,
时,![]() 随
随![]() 增大而增大;当
增大而增大;当![]() 时,
时,![]() 随
随![]() 增大而减小.
增大而减小.
【解析】
(1)设二次函数解析式为y=a(x﹣1)(x﹣2),然后把点(3,4)代入函数解析式求得a的值即可;
(2)将(1)中抛物线的解析式利用配方法转化为顶点式,可以直接写出顶点坐标;
(3)根据抛物线的开口方向和对称轴写出答案.
(1)∵二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),
∴设该二次函数解析式为y=a(x﹣1)(x﹣2)(a≠0),
把点(3,4)代入,得:
a×(3﹣1)×(3﹣2)=4,
解得:a=2.
则该抛物线的解析式为:y=2(x﹣1)(x﹣2);
(2)由(1)知,抛物线的解析式为y=2(x﹣1)(x﹣2).
∵y=2(x﹣1)(x﹣2)=2(x![]() )2
)2![]() ,
,
∴该抛物线的顶点坐标是:(![]() ,
,![]() ).
).
(3)由抛物线的解析式y=2(x![]() )2
)2![]() 知,抛物线开口方向向上,对称轴是x
知,抛物线开口方向向上,对称轴是x![]() .
.
结合二次函数y=ax2+bx+c的图象与x轴交于点(1,0)和(2,0),作出该抛物线的大致图象.
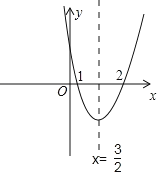
如图所示,当x![]() 时,y随x的增大而增大;当x
时,y随x的增大而增大;当x![]() 时,y随x的增大而减小.
时,y随x的增大而减小.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=30,AD=20,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为调查市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :电动车,
:电动车,![]() :公交车,
:公交车,![]() :家庭汽车,
:家庭汽车,![]() :其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
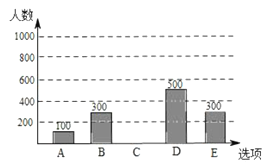
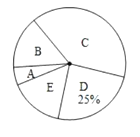
(1)本次调查中,一共调查了 名市民,其中“![]() :公交车”选项的有 人;扇形统计图中,
:公交车”选项的有 人;扇形统计图中,![]() 项对应的扇形圆心角是 度;
项对应的扇形圆心角是 度;
(2)若甲、乙两人上班时从![]() 、
、![]() 、
、![]() 、
、![]() 四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
(1)求y与x的函数解析式;
(2)设该水果销售店试销草莓获得的利润为W元,求W的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAB与△OCD是以点0为位似中心的位似图形,相似比为1:2,∠OCD=90![]() ,CO=CD.若B(2,0),则点C的坐标为( )
,CO=CD.若B(2,0),则点C的坐标为( )
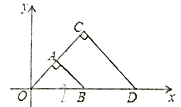
A. (2,2) B. (1,2) C. (![]() ,2
,2![]() ) D. (2,1)
) D. (2,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为反比例函数y=![]() (k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
(k>0)在第一象限内图象上的一点,过点P分别作x轴,y轴的垂线交一次函数y=﹣x﹣4的图象于点A、B.若∠AOB=135°,则k的值是( )
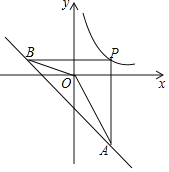
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在函数y=![]() (x>0)的图象上,过点A作x轴、y轴的垂线分别交函数y=
(x>0)的图象上,过点A作x轴、y轴的垂线分别交函数y=![]() (x>0,k>2)的图象于点B、C,过点C作x轴的垂线交y=
(x>0,k>2)的图象于点B、C,过点C作x轴的垂线交y=![]() (x>0)的图象于点D,连结BC、OC、OD.若点A、C的横坐标分别为1和2,则△ABC与△OCD的面积之和为( )
(x>0)的图象于点D,连结BC、OC、OD.若点A、C的横坐标分别为1和2,则△ABC与△OCD的面积之和为( )
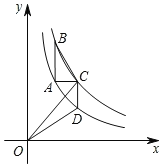
A.2B.3C.4D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校准备组织一次“研学之旅”活动,现用抽签的方式从以下四个地方:九峰公园、柑橘博览园、平田桐树坑、长潭水库(其中九峰公园、平田桐树坑是爱国主义教育基地)中确定两个作为活动地点.将四个地点分别写在4张完全相同的卡片上,背面朝上并洗匀,先从中随机抽取一张卡片,再从剩下的卡片中随机抽取一张.则“抽中的两个地方都是爱国主义教育基地”的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在![]() 中,
中,![]() ,
,![]() ,D是BC的中点.
,D是BC的中点.
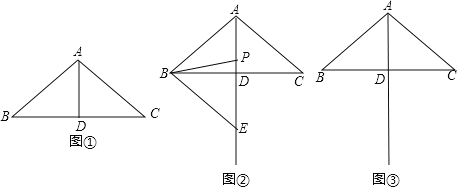
小明对图①进行了如下探究:在线段AD上任取一点P,连接PB.将线段PB绕点P按逆时针方向旋转![]() ,点B的对应点是点E,连接BE,得到
,点B的对应点是点E,连接BE,得到![]() .小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
.小明发现,随着点P在线段AD上位置的变化,点E的位置也在变化,点E可能在直线AD的左侧,也可能在直线AD上,还可能在直线AD的右侧.请你帮助小明继续探究,并解答下列问题:
(1)当点E在直线AD上时,如图②所示.
①![]() ;②连接CE,直线CE与直线AB的位置关系是 .
;②连接CE,直线CE与直线AB的位置关系是 .
(2)请在图③中画出![]() ,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
,使点E在直线AD的右侧,连接CE.试判断直线CE与直线AB的位置关系,并说明理由.
(3)当点P在线段AD上运动时,求AE的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com