
【题目】如图,在Rt△ABC中,∠B=90°,AC=10cm,BC=6cm,现有两点P,Q分别从点A和点C同时出发,沿边AB,CB向终点B移动.其中点P,Q的速度分别为2cm/s,1cm/s,且当其中一点到达终点时,另一点也随之停止移动.设P,Q两点移动时间为x s.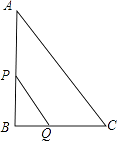
(1)用含x的代数式表示BQ、BP的长度,并求x的取值范围.
(2)设四边形APQC的面积为y(cm2),求y与x的函数关系式?
(3)是否存在这样的x,使得四边形APQC的面积是△ABC面积的 ![]() ?如果存在,求出x的值;不存在请说明理由.
?如果存在,求出x的值;不存在请说明理由.
【答案】
(1)
解:∵∠B=90°,AC=10,BC=6,
∴AB=8.
∴BQ=6﹣x,PB=8﹣2x
(2)
解:由题意,得
y=S四边形APQC=S△ABC﹣SPBQ
= ![]() ABBC﹣
ABBC﹣ ![]() PBQB
PBQB
= ![]() ×6×8﹣
×6×8﹣ ![]() (6﹣x)(8﹣2x)
(6﹣x)(8﹣2x)
=24﹣(x2﹣10x+24)
=﹣x2+10x
(3)
解:假设存在x的值,使得四边形APQC的面积是△ABC面积的 ![]() ,
,
则﹣x2+10x= ![]() ×6×8×
×6×8× ![]() ,
,
解得x1=2,x2=8(舍去).
假设成立,所以当x=8时,四边形APQC的面积是△ABC面积的 ![]()
【解析】(1)首先运用勾股定理求出AB边的长度,然后根据路程=速度×时间,分别表示出BQ、PB的长度;(2)利用y=S四边形APQC=S△ABC﹣SPBQ求解即可;(3)根据四边形APQC的面积=△ABC的面积﹣△PBQ的面积,列出方程,根据解的情况即可判断.
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() 的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).
的图象与一次函数y=ax+b的图象交于点A(﹣2,3)和点B(m,﹣2).
(1)求反比例函数和一次函数的解析式;
(2)直线x=1上有一点P,反比例函数图象上有一点Q,若以A、B、P、Q为顶点的四边形是以AB为边的平行四边形,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,PE,PF分别交AB,AC于点E,F,给出下列四个结论:①△APE≌△CPF;②AE=CF;③△EAF是等腰直角三角形;④S△ABC=2S四边形AEPF,上述结论正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”长假期间,小张和小李决定骑自行车外出旅游,两人相约一早从各自家中出发,已知两家相距10千米,小张出发必过小李家.
(1)若两人同时出发,小张车速为20千米,小李车速为15千米,经过多少小时能相遇?
(2)若小李的车速为10千米,小张提前20分钟出发,两人商定小李出发后半小时二人相遇,则小张的车速应为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划在“阳光体育”活动课程中开设乒乓球、羽毛球、篮球、足球四个体育活动项目供学生选择.为了估计全校学生对这四个活动项目的选择情况,体育老师从全体学生中随机抽取了部分学生进行调查(规定每人必须并且只能选择其中的一个项目),并把调查结果绘制成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
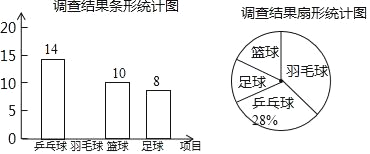
(1)求参加这次调查的学生人数,并补全条形统计图;
(2)求扇形统计图中“篮球”项目所对应扇形的圆心角度数;
(3)若该校共有600名学生,试估计该校选择“足球”项目的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A的坐标为(4,0),点B从原点出发,沿y轴负方向以每秒1个单位长度的速度运动,分别以OB,AB为直角边在第三、第四象限作等腰Rt△OBE,等腰Rt△ABF,连结EF交y轴于P点,当点B在y轴上运动时,经过t秒时,点E的坐标是_____(用含t的代数式表示),PB的长是_____.
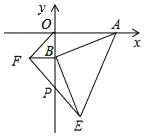
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com