
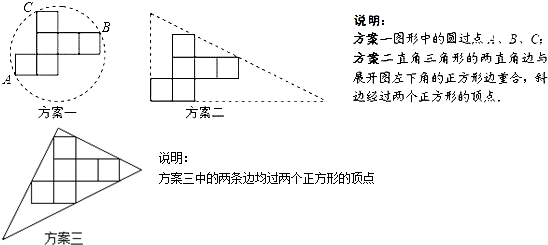
分析 (1)连接AC、BC、AB,由AC=BC=$\sqrt{5}$,AB=$\sqrt{10}$,根据勾股定理的逆定理,即可求得∠BAC=90°,又由90°的圆周角所对的弦是直径,则可证得AB为该圆的直径;
(2)首先证得△ADE≌△EHF与△ADE∽△ACB,即可求得AD与BC的长,求得△ABC的面积,即可求得该方案纸片利用率;
(3)利用方案(2)的方法,分析求解即可求得答案.
解答 解:发现:(1)小明的这个发现正确.
理由:
解法一:如图1,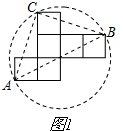
连接AC、BC、AB,
∵AC=BC=$\sqrt{10}$,AB=2$\sqrt{5}$
∴AC2+BC2=AB2,
∴∠BCA=90°,
∴AB为该圆的直径.
解法二:如图2,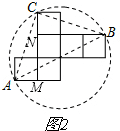
连接AC、BC、AB.
易证△AMC≌△BNC,
∴∠ACM=∠CBN.
又∵∠BCN+∠CBN=90°,
∴∠BCN+∠ACM=90°,
即∠BCA=90°,
∴AB为该圆的直径.
(2)如图3,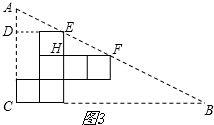
∵DE=FH,DE∥FH,
∴∠AED=∠EFH,
∵∠ADE=∠EHF=90°,
∴△ADE≌△EHF(ASA),
∴AD=EH=1.
∵DE∥BC,
∴△ADE∽△ACB,
∴$\frac{AD}{AC}$=$\frac{DE}{CB}$,
∴$\frac{1}{4}$=$\frac{2}{CB}$,
∴BC=8,
∴S△ACB=16.
∴该方案纸片利用率=$\frac{展开图的面积}{纸板的总面积}$×100%=×100%=37.5%;
探究:
(3)如图4,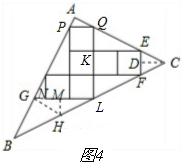
过点C作CD⊥EF于D,过点G作GH∥AC,交BC于点H,
设AP=a,
∵PQ∥EK,
∴△APQ∽△KQE,△CEF是等腰三角形,△GHL是等腰三角形,
∴$\frac{AP}{AQ}=\frac{AQ}{EK}$=$\frac{1}{2}$,
∴AQ=2a,PQ=a$\sqrt{5}$,
∴EQ=5a,
∵EC:ED=QE:QK,
∴EC=$\frac{5}{2}$a,
则PG=5a+$\frac{5}{2}$a=$\frac{15}{2}$a,GL=$\frac{5\sqrt{5}}{2}$a,
∴GH=$\frac{25}{8}$a,
∵$\frac{GH}{2a+5a+\frac{5}{2}a}=\frac{GB}{GB+\frac{15}{2}a+a}$,
解得:GB=$\frac{25}{6}$a,
∴AB=$\frac{38}{3}$a,AC=$\frac{19}{2}$a,
∴S△ABC=$\frac{1}{2}$×AB×AC=$\frac{361}{6}$a2,
S展开图面积=6×5a2=30a2,
∴该方案纸片利用率=$\frac{展开图的面积}{纸板的总面积}$×100%=$\frac{180}{361}$×100%=49.86%.
点评 此题是圆的综合题,主要考查了全等三角形的性质和判定,相似三角形的性质和判定,勾股定理,勾股定理的逆定理,圆周角的性质,解本题的关键是用相似和全等,勾股定理表示线段.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com