
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.
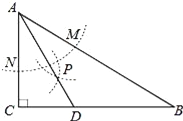
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】试题分析:由角平分线的作法可知AD是BAC的平分线,由直角三角形两锐角互余可知∠CAB=60°,从而可知∠BAD=30°,由此可将∠BAD=∠B=30°,从而得到AD=DB,根据到线段两端距离相等的点在线段的垂直平分线上可判断③;由三角形的外角的性质可知∠ADC=∠B+∠BAD可判断.
解:由角平分线的作法可知①正确;
∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD是∠BAC的平分线,
∴∠BAD=30°.
∴∠BAD=∠B=30°.
∴AD=DB.
∴点D在AB的垂直平分线上.
∴③正确.
∵∠ADC=∠B+∠BAD,
∴∠ADC=30°+30°=60°.
故②正确.
故选:D.


科目:初中数学 来源: 题型:
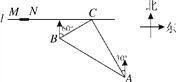
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OP是∠BOC的平分线,OE⊥AB,OF⊥CD.

(1)图中除直角和平角外,还有相等的角吗?请写出两对:
① ;② .
(2)如果∠AOD=40°,求∠COP和∠BOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
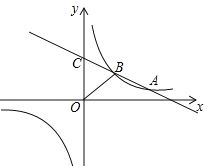
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,O是对角线AC上一点,点E在BC的延长线上,且OE = OB.
(1)求证:△OBC ≌ △ODC.
(2)求证:∠DOE = ∠ABC.
(3)把正方形ABCD改为菱形,其他条件不变(如图2),若∠ABC = 52° ,求∠DOE的度数.
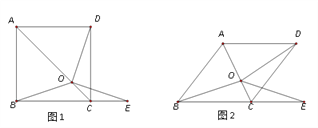
查看答案和解析>>
科目:初中数学 来源: 题型:
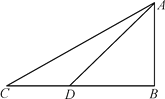
【题目】如图,某校数学兴趣小组为测得校园里旗杆AB的高度,在操场的平地上选择一点C,测得旗杆顶端A的仰角为30,再向旗杆的方向前进16米,到达点D处(C,D,B三点在同一直线上),又测得旗杆顶端A的仰角为45,请计算旗杆AB的高度(结果保留根号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com