
【题目】如图,△ABC中,AB=AC,AD、AE分别是∠BAC与∠BAC的外角的平分线,BE⊥AE.求证:AB=DE

【答案】证明见解析.
【解析】试题分析:先由角平分线和等腰三角形的性质证明AE∥BD,再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE,可得AD∥BE,可证得四边形ADBE为矩形,可得结论.
试题解析:证明:∵AD、AE分别是∠BAC与∠BAC的外角的平分线,∴∠BAD+∠EAB=![]() (∠BAC+∠FAB)=90°,∵BE⊥AE,∴DA∥BE,∵AB=AC,∴∠ABC=∠ACB,∵∠FAB=∠ABC+∠ACB=2∠ABC,且∠FAB=2∠EAB,∴∠ABC=∠EAB,∴AE∥BD,∴四边形AEBD为平行四边形,且∠BEA=90°,∴四边形AEBD为矩形,∴AB=DE.
(∠BAC+∠FAB)=90°,∵BE⊥AE,∴DA∥BE,∵AB=AC,∴∠ABC=∠ACB,∵∠FAB=∠ABC+∠ACB=2∠ABC,且∠FAB=2∠EAB,∴∠ABC=∠EAB,∴AE∥BD,∴四边形AEBD为平行四边形,且∠BEA=90°,∴四边形AEBD为矩形,∴AB=DE.


科目:初中数学 来源: 题型:
【题目】矩形的一个内角平分线把矩形的一条边分成3cm和5cm两部分,则矩形的周长( )

A.16cm B.22cm和16cm C.26cm D.22cm和26cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数y=x2+2x﹣3的图象如图所示,点A(x1,y1),B(x2,y2)是该二次函数图象上的两点,其中﹣3≤x1<x2≤0,则下列结论正确的是( )
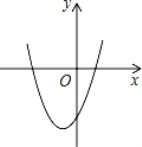
A. y1<y2B.y1>y2C.y的最小值是﹣3 D.y的最小值是﹣4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21.动点P从点D出发,沿射线DA的方向以每秒2个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动.设运动的时间为t(秒).
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B、P、Q三点为顶底的三角形是等腰三角形?
(3)当线段PQ与线段AB相交于点O,且2AO=OB时,求∠BQP的正切值;
(4)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用公式法解下列方程
(1)x=4x2+2 (2)-x 2+5x-4=0
(3)7x2 -28x +7= 0 (4)(x+1)(x+8)=-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是()
A. “明天降雨的概率为50%”,意味着明天一定有半天都在降雨
B. 了解全国快递包裹产生的包装垃圾数量适合采用全面调查(普查)方式
C. 掷一枚质地均匀的骰子,骰子停止转动后,6点朝上是必然事件
D. —组数据的方差越大,则这组数据的波动也越大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com