
【题目】如图,矩形ABCD中,点P是线段AD上一动点,O为BD的中点,PO的延长线交BC于Q. 
(1)求证:OP=OQ;
(2)若AD=8厘米,AB=6厘米,P从点A出发,以1厘米/秒的速度向D运动(不与D重合).设点P运动时间为t秒,请用t表示PD的长;并求t为何值时,四边形PBQD是菱形.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,
∴∠PDO=∠QBO,
又∵O为BD的中点,
∴OB=OD,
在△POD与△QOB中,
∵ 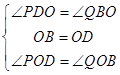
∴△POD≌△QOB(ASA),
∴OP=OQ;
(2)解:PD=8﹣t,
∵四边形PBQD是菱形,
∴PD=BP=8﹣t,
∵四边形ABCD是矩形,
∴∠A=90°,
在Rt△ABP中,由勾股定理得:AB2+AP2=BP2,
即62+t2=(8﹣t)2,
解得:t= ![]() ,
,
即运动时间为 ![]() 秒时,四边形PBQD是菱形.
秒时,四边形PBQD是菱形.
【解析】(1)本题需先根据四边形ABCD是矩形,得出AD∥BC,∠PDO=∠QBO,再根据O为BD的中点得出△POD≌△QOB,即可证出OP=OQ.(2)本题需先根据已知条件得出∠A的度数,再根据AD=8厘米,AB=6厘米,得出BD和OD的长,再根据四边形PBQD是菱形时,即可求出t的值,判断出四边形PBQD是菱形.
【考点精析】关于本题考查的勾股定理的概念和菱形的性质,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半才能得出正确答案.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】为了了解中学生的体能情况,我校随机抽取了九年级男生50名,进行立定跳远测试,将所得数据按成绩![]() 单位:米
单位:米![]() 高低绘制成频数分布直方图,如图所示,其中按成绩分组前四个小组的频率依次为
高低绘制成频数分布直方图,如图所示,其中按成绩分组前四个小组的频率依次为![]() ,完成下列问题
,完成下列问题![]() 注:图中成绩数据含低值不含高值
注:图中成绩数据含低值不含高值![]()

![]() 第四小组的频数是多少?
第四小组的频数是多少?
![]() 补全统计图;
补全统计图;
![]() 规定成绩在
规定成绩在![]() 米以上为及格,
米以上为及格, ![]() 米以上为优秀,测试的学生的及格率是多少?优秀率是多少?
米以上为优秀,测试的学生的及格率是多少?优秀率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .

(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次函数y=x2的图象沿着x轴向右平移2个单位,再向上平移3个单位,所得到的函数图象的解析式为( )
A.y=(x+2)2+3
B.y=(x﹣2)2+3
C.y=(x+2)2﹣3
D.y=(x﹣2)2﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,矩形ABCD中,O为AC中点,过点O的直线分别与AB、CD交于点E、F,连结BF交AC于点M,连结DE、BO.若∠COB=60°,FO=FC,则下列结论:①FB垂直平分OC;②△EOB≌△CMB;③DE=EF;④S△AOE:S△BCM=2:3.其中正确结论的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中,①两条直线被第三条直线所截,同位角相等;②同角的余角相等;③负数有一个立方根;④相等的角是对顶角;假命题有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com