
分析 (1)令x=0,则y=c,再根据OC=3,可求点C的坐标,把C(0,-3)代入y2=-3x+t可求t的值;
(2)把A(x1,0)代入,y2=-3x-3,可求A(-1,0),进一步得到B(3,0),再待定系数法可求自变量x的取值范围;
(3)根据两个函数的交点坐标即可得到自变量x的取值范围.
解答 解:(1)令x=0,则y=c,
∴C(0,c),
∵OC=3,
∴|c|=3,即c=±3,
又∵c<0,
∴c=-3,
∴C(0,-3),
把C(0,-3)代入y2=-3x+t,则0+t=-3,即t=-3;
(2)∵t=-3,
∴y2=-3x-3,
把A(x1,0)代入,y2=-3x-3,则-3x1-3=0,即x1=-1,
∴A(-1,0),
∵x1x2异号,x1=-1<0∴x2>0,
∵|x1|+|x2|=4,
∴1+x2=4,x2=3,则B(3,0),
代入${y_1}=a{x^2}+bx-3$得$\left\{\begin{array}{l}a-b-3=0\\ 9a+3b-3=0\end{array}\right.$,
解得:$\left\{\begin{array}{l}a=1\\ b=-2\end{array}\right.$,
${y_1}={x^2}-2x-3={(x-1)^2}-4$,
则当x≤1 时,y随x增大而减小.
∴当y随x增大而减小时,x≤1;
(3)若y1>y2,自变量x的取值范围为x<-1或x>0.
点评 此题主要考查了二次函数与不等式(组),抛物线与x轴的交点,以及求两函数的交点坐标以及比较函数值的大小等知识,利用数形结合比较函数值的大小是这部分考查的重点.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | 0 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
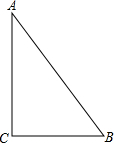 如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
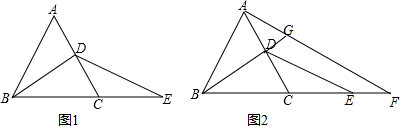
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
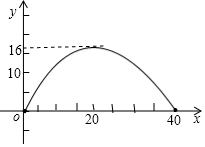 如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.
如图建立直角坐标系,某抛物线型桥拱的最大高度为16米,跨度为40米,则它对应的解析式为:y=-$\frac{1}{25}$x2+$\frac{2}{5}$x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com