
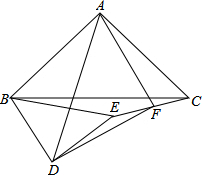
 已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形.
已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形. 分析 如图,延长AF到M,使得FM=AF,连接EM,DM.先证明△AFC≌△MFE,得出AC=EM=AB,再证明△ABD≌△MED,推出△ADM是等腰直角三角形即可解决问题.
解答 证明:如图,延长AF到M,使得FM=AF,连接EM,DM.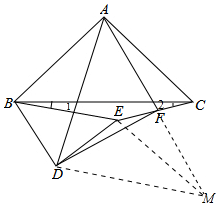
∵△ABC,△BDE都是等腰直角三角形,
∴AB=AC,BD=DE,∠ABC=∠ACB=∠DBE=∠DEB=45°,
在△AFC和△MFE中,
$\left\{\begin{array}{l}{AF=FM}\\{∠AFC=∠EFM}\\{CF=EF}\end{array}\right.$,
∴△AFC≌△MFE,
∴AC=EM=AB,∠MEF=∠ACE,
∵∠DEM=360°-∠DEB-∠MEF-∠BEC=360°-45°-(45°+∠2)-(180°-∠1-∠2)=90°+∠1=∠ABC+∠1+∠DBE=∠ABD,
在△ABD和△MED中,
$\left\{\begin{array}{l}{AB=EM}\\{∠ABD=∠DEM}\\{BD=DE}\end{array}\right.$,
∴△ABD≌△MED,
∴AD=DM,∠BDA=∠MDE,
∴∠ADM=∠BDE=90°,∵AF=FM,
∴DF=AF=FM,DF⊥AM,
∴△ADF是等腰直角三角形.
点评 本题主要考查了全等三角形的判定与性质,直角三角形斜边上的中线等于斜边的一半的性质,等腰直角三角形的性质,在本题中需要作辅助线来证明,难度较大.熟练掌握判定定理及性质并灵活运用是解题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 收入20元与支出30元 | B. | 上升了6米和后退了7米 | ||
| C. | 卖出10斤米和盈利10元 | D. | 向东行30米和向北行30米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,对角线AC与BD相交于点O,AB=4$\sqrt{2}$,AC=4,BD=12,点P是线段AD上的动点(不包含端点A、D),过点P作PE⊥AC,PF⊥BD,垂足分别为点E,F
如图,在?ABCD中,对角线AC与BD相交于点O,AB=4$\sqrt{2}$,AC=4,BD=12,点P是线段AD上的动点(不包含端点A、D),过点P作PE⊥AC,PF⊥BD,垂足分别为点E,F查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com