
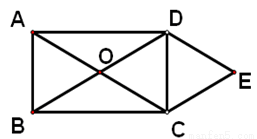
如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD。
(1)试判断四边形OCED是何种特殊四边形,并加以证明.
(2)若∠OAD=300,F、G分别在OD、DE上,OF=DG,连结CF、CG、FG, 判断△CFG形状,并加以证明.
(1)菱形,证明见解析;(2)等边三角形,证明见解析.
【解析】
试题分析:(1)根据矩形性质求出OC=OD,根据平行四边形的判定得出四边形OCED是平行四边形,根据菱形判定推出即可;
(2)判断出△OCD和△CDE是等边三角形,根据等边三角形的性质可得∠COD=∠CDG=60°,再利用“边角边”证明△COF和△CDG全等,根据全等三角形对应边相等可得CF=CG全等三角形对应角相等可得∠DCG=∠OCF,再求出∠FCG=60°,然后判断出△CFG是等边三角形.
试题解析:(1)证明:∵四边形ABCD是矩形,
∴AC=2OC,BD=2OD,AC=BD,
∴OD=OC,
∵DE∥AC,CE∥BD,
∴四边形OCED是菱形.
(2)在矩形ABCD中,△OCD和△CDE是等边三角形,

∴∠COD=∠CDG=60°,
在△COF和△CDG,
 ,
,
∴△COF≌△CDG(SAS),
∴CF=CG,∠DCG=∠OCF,
∴∠FCG=∠DCO=60°,
∴△CFG为等边三角形.
考点:1.矩形的性质;2.菱形的判定.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请直接写出点Q 坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:选择题
计算(a3b)2÷(ab)2的结果是 ( )
A.a3 B.a4 C.a3b D.a4b
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:填空题
已知关于x的一元二次方程x2+bx+b﹣1=0有两个相等的实数根,则b的值是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:解答题
如图,某广场一灯柱AB被一钢缆CD固定,CD与地面成37°夹角,且CB=4米.
(1)求钢缆CD的长度;
(2)若AD=2.1米,灯的顶端E距离A处1.8米,且∠EAB=120°,则灯的顶端E距离地面多少米? (参考数据:sing37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏大丰刘庄第二初中九年级下学期第一次月考数学试卷(解析版) 题型:选择题
一个反比例函数的图象经过点(2,3),则这个反比例函数的解析式为( )
A. B.
B.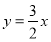 C.
C.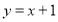 D.
D.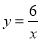
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com