
如图,在平面直角坐标系中,△ABC 的顶点坐标分别为A(-2,0)、B(4,0)、C(0,2).
(1)请用尺规作出△ABC的外接圆⊙P(保留作图痕迹,不写作法);
(2)求出(1)中外接圆圆心P的坐标;
(3)⊙P上是否存在一点Q,使得△QBC与△AOC相似?如果存在,请直接写出点Q 坐标;如果不存在,请说明理由.

(1)作图见解析;(2)点P坐标为(1,-1).(3)⊙P上存在一点Q(-2,-2),(2,-4),使得△QBC与△AOC相似.
【解析】
试题分析:(1)作出AC与BC线段垂直平分线得出交点即为圆心,进而利用圆心到线段端点距离长为半径求出即可;
(2)过点P做PD⊥x轴,PE⊥y轴,垂足分别为D、E,连接PC、PE,在Rt△BPD中,BP2=x2+32,在Rt△CEP中,CP2=(x+2)2+12,由BP=CP,求出x的值,即可得出P点坐标;
(3)利用相似三角形的判定得出△Q1BC∽△ACO,进而结合圆周角定理得出Q点坐标.
(1)如图1所示:
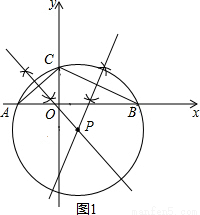
(2)如图2,过点P做PD⊥x轴,PE⊥y轴,垂足分别为D、E,连接PC、PE.
∵PD⊥AB,∴AD=BD=3.
∵OB=4,∴OD=OB-BD=1.
∴PE=OD=1.
设DP=x,则OE=PD=x.
在Rt△BPD中,BP2=x2+32.
在Rt△CEP中,CP2=(x+2)2+12.
∵BP=CP,
∴x2+32=(x+2)2+12.
解得:x=1.
∴点P坐标为(1,-1).
(3)如图2,连接BP并延长到⊙P于一点Q1,连接CQ1,

则BQ1是直径,
∴∠Q1CB=90°,
又∵∠CAB=∠CQ1B,
∴△Q1BC∽△ACO,
此时连接AQ1则∠Q1AB=90°,
∴Q1横坐标为:-2,
∵AB=6,BQ1=2BP=2 ,
,
∴AQ1=2,
∴Q1(-2,-2),
同理构造直角三角形CFQ2,
可得出:CF=6,CQ2=2 ,
,
∴FQ2=2,FO=4,
则Q2(2,-4),
综上所述:⊙P上存在一点Q(-2,-2),(2,-4),使得△QBC与△AOC相似.
考点:圆的综合题.


科目:初中数学 来源:2013-2014学年江苏省南京市溧水区中考一模数学试卷(解析版) 题型:填空题
如 图,在边长为3 cm的正方形ABCD中,点E为BC边上的任意一点,AF⊥AE,AF交CD的延长线于F,则四边形AFCE的面积为 cm2.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
南京市为了构建立体的道路网络,大力发展江北经济,决定修建一条六合到主城的轻轨铁路.为了使工程提前3个月完成,需将原定的工作效率提高10%.原计划完成这项工程需要多少个月?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:填空题
在函数y=- 的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .
的图象上有三个点为(x1,y1)、(x2,y2)、(x3,y3),若y1<0<y2<y3,则x1,x2,x3的大小关系是 .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:解答题
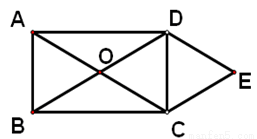
如图,矩形ABCD中,对角线AC、BD交于点O,DE∥AC,CE∥BD。
(1)试判断四边形OCED是何种特殊四边形,并加以证明.
(2)若∠OAD=300,F、G分别在OD、DE上,OF=DG,连结CF、CG、FG, 判断△CFG形状,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com